68. По данным на рисунке найдите площадь 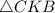 .
.
ΔСКВ - прямоугольный (∠С = 90°).
СК - высота (СК⊥АВ).
АК = 4, КВ = 16.
Найти :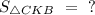 Решение :В прямоугольном треугольнике высота, проведённая к гипотенузе - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.
Решение :В прямоугольном треугольнике высота, проведённая к гипотенузе - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.Следовательно, 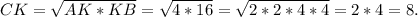
Следовательно, 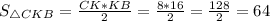 ед².
ед².
64 ед².
- - -70. ABCD - прямоугольник. Найдите 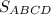 .
.
Четырёхугольник ABCD - прямоугольник.
АС - диагональ.
HD⊥АС.
HD = 6, АН = 9.
Найти :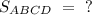
Следовательно ∠D = 90°.
Рассмотрим ΔACD - прямоугольный.
В прямоугольном треугольнике высота, опущенная на гипотенузу - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.Следовательно, 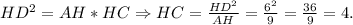
Следовательно, 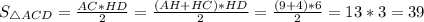 ед².
ед².
Тогда 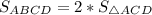 = 2*39 ед² = 78 ед².
= 2*39 ед² = 78 ед².
78 ед².
SΔ=(1/2)*a*a*sin 120°, SΔ=(1/2)*a² *(√3/2)
64√3=(1/4)a²√3, a²=256, a=16
основание Δ обозначим с.
рассмотрим прямоугольный Δ, образованный высотой треугольника, боковой стороной и половиной основания.
cos 30°=(c/2)/a
√3/2=(c/2)/16, √3/2=c/32, c=16√3
ответ: стороны треугольника 16 см, 16см, 16√3 см
рассмотрим прямоугольный Δ, образованный высотой треугольника h, боковой стороной а и половиной основания с/2.
пусть h=х см, тогда а=2х см(катет против угла 30 в 2 раза меньше гипотенузы)
по т. Пифагора: (2х)²=(с/2)²+х². 4х²=с²/4+х², с²/4=3х². с²=12х², с=2х√3
SΔ=(1/2)*c*h
64√3=(1/2)*2x√3*x
64√3=x² √3, x²=64, x=8, => h=8 см, а=2*8=16 см, с=2*8*√3=16√3 см
ответ: 16,16 и 16√3