Пусть этот треугольник будет АВС, где АВ и АС это катеты, а ВС - гипотенуза. Так как один угол в прямоугольном треугольнике равен 60, то другой 90-60=30 Значит, что данный треугольник - это половина равностороннего треугольника ДВС (у которого все стороны и углы равны) и меньший катет АС - это будет половина стороны ВС, так как больший катет АВ является одновременно и высотой и медианой равностороннего треугольника ДВС. Тогда пусть катет АС будет х, тогда гипотенуза ВС будет 2х, а их сумму мы знаем и составляем уравнение: х+2х=96 3х=96 х=32 см (это длина катета АС) тогда длина гипотенузы ВС будет 32*2=64 см
1) 2²+2²=√8
х=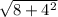 =√24=2√6
=√24=2√6
2)10²-6²=√64=8
х²+х²=8²
2х²=64
х²=32
х=4√2
3) 21²-12²=441-144=√297=3√33
х=(3√33)²+24²=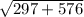 =√873=3√97
=√873=3√97
4)12²-5²=√119
х=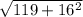 =√375=5√15
=√375=5√15
5) 3²+2²=√13
х=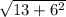 =√49=7
=√49=7
Объяснение: