Составьте уравнение прямой, проходящей через точки А(-1; 4) и В(3; – 8).
Запишите уравнение прямой, изображенной на рисунке 11.
У.
у.
(4;5)
(-2; 5)
0
А
(-2;-1)
0
а)
Puc. 12
Докажите, что данное уравнение является уравнением округе
ности, и укажите координаты центра и радиус этой окружности:
1) x2+y2 - 2x – 4y-7= 0; 2) x2+y2 -8y = 0.
Найдите координаты точки пересечения прямых 9х+5y=1
2x + 3y = 8.
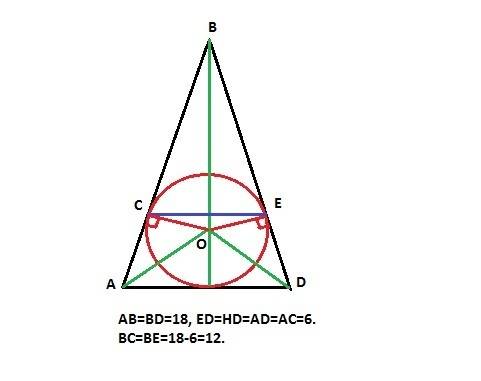
ВК=2, АК=8, тогда, АВ=10.
Центр вписанной окружности лежит в точке пересечения биссектрис треугольника, проведём биссектрису ВН: точка Н совпадёт с точкой касания окружности на стороне АС, т.к. в биссектриса, проведённая из угла В, является и высотой, и медианой, т.е. угол АНС = 90 градусов.
АН=АК, т.к. отрезки касательных, проведённых из одной точки, равны, т.е. АН=8, тогда АС=16.
В прямоугольном треугольнике АВН АВ=10, АН=8, тогда по теореме Пифагора ВН=6.
Найдём площадь треугольника: 1/2 * АС * ВН = 1/2 * 16 * 6 = 42.