1 случай, где катет ВС = 4,2 см
Если катет равен половине гипотенузы, то напротив лежащий угол равен 30°.
=> ∠А = 30°.
Сумма острых углов прямоугольного треугольника равна 90°.
∠В = 90° - 30° = 60°
ответ: 60°, 30°.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
2 случай, где АС = 4,2 см.
Если катет равен половине гипотенузы, то напротив лежащий угол равен 30°.
=> ∠В = 30°
Сумма острых углов прямоугольного треугольника равна 90°.
∠А = 90° - 30° = 60°
ответ: 30°, 60°.
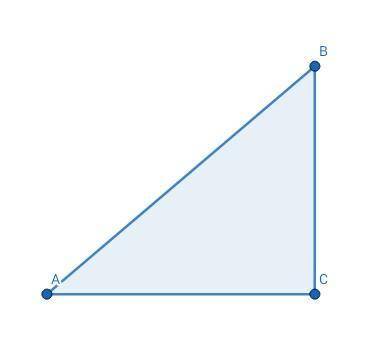
Углы при основании равны по 45°, угол при вершине 90°
Объяснение:
Пусть угол при основании равнобедренного треугольника равен х, тогда внешний угол при основании равнобедренного треугольника равен 3х.
Эти углы смежные, их сумма равна 180°.
х + 3х = 180°
4х = 180°
х = 45° - угол при основании
3х = 3 · 45° = 135° внешний угол при основании
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
Внешний угол при основании равнобедренного треугольника равен 135°, один из не смежных с ним углов при основании равен 45°, тогда угол при вершине равен
135° - 45° = 90°.
Объяснение:
<А=30 градусов
S=150 см^2
Найти : боковую сторону b=?
S=1/2×b^2×sinA
150=1/2×b^2×sin30
300=b^2×1/2
b=корень (300:1/2)=корень (300×2)=
=корень 600=10корень6 (см)
ответ : b=10корень6 (см)