В прямоугольнике все углы прямые, противоположные стороны равны и параллельны, а диагонали равны и точкой пересечения делятся пополам.
Пусть данный прямоугольник АВСD, точки К, М, Н, Т - соответственно середины АВ, ВС, СD, DА.
Соединим последовательно точки К,М,Н и Т
Треугольники КАТ, КВМ, МСН и НDТ прямоугольные, в каждом один катет равен половине меньшей стороны, другой - половине большей стороны. Следовательно, эти треугольники равны, отсюда равны их гипотенузы: КМ=МН=НТ=ТК.
КМНТ - четырехугольник, все стороны которого равны (признак ромба).
Кроме того: диагонали КН║ВС и МТ║АВ.
В прямоугольнике стороны пересекаются под прямым углом, ⇒
параллельные им диагонали ромба КН и МТ тоже пересекаются под прямым углом - признак ромба.
Четырехугольник КМНТ - ромб, и его вершинами являются середины сторон прямоугольника.

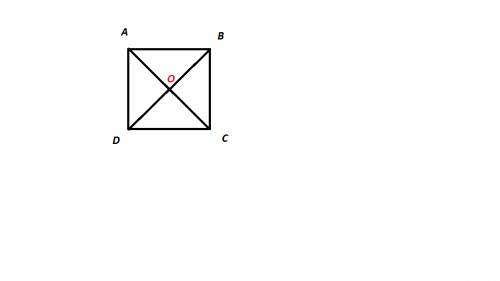
Точка D и C а так же О, лежат в плоскости.
РАссмотрим диагонал DB. B пренадлежит DO, а DO лежит в плоскости(так как две точки лежат в плоскости) => B лежит в плоскости.
Рассмотрим диагонал CA. A пренадлежит СO, а СО лежит в плоскости(так как две точки С и О лежат в плоскости) следовательно А лежит также в плоскости.
следовательно все вершины квадрата находятся в одной плоскости
это на основе теоремы: ЕСЛИ ДВЕ ТОЧКИ ПРЯМОЙ ЛЕЖАТ В ПЛОСКОСТИ,ТО ВСЕ ТОЧКИ ПРЯМОЙ ЛЕЖАТ В ЭТОЙ ПЛОСКОСТИ. вроде так звучит, удачи вам.