BC = 16/(2√3 - 1) см.
Объяснение:
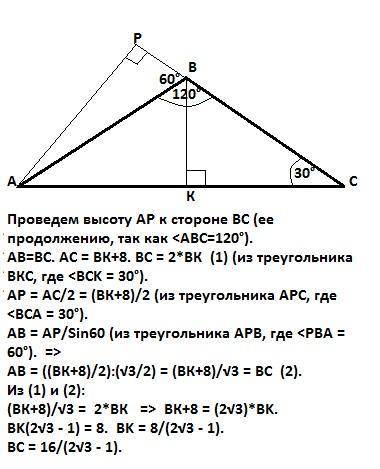
Треугольник АВС равнобедренный, медиана ВК является и высотой, и биссектрисой. (см. рисунок в задании).
Проведем высоту АР к стороне ВС (ее продолжению, так как ∠<ABC=120°), АВ=ВС, АС = ВК+8см (дано).
ВС = 2*ВК (1) (из треугольника ВКС, где ∠BKC=90°, a ∠BCK=30°).
АР = АС/2 = (ВК+8)/2 (из треугольника АРС где ∠APC=90°, a ∠BCA=30°).
АВ = АР/Sin60 (из треугольника АРB, где ∠APB=90°, a ∠РBA=60°, а
Sin(∠PBA = AP/AB). Sin60 = √3/2 =>
АВ = ((ВК+8)/2):(√3/2) = (ВК+8)/√3 = ВС (2).
Из (1) и (2):
(ВК+8)/√3 = 2*ВК => ВК+8 = (2√3)*BK.
BK(2√3 - 1) = 8. BK = 8/(2√3 - 1).
BC = 16/(2√3 - 1)см.
Через катет прямоугольного равнобедренного треугольника проведена плоскость, которая образует с плоскостью треугольника угол 60°. Найдите углы, которые образуют 2 другие стороны треугольника с этой плоскостью.
Обозначим треугольник АВС. АС=ВС, угол С=90°
Проведенная плоскость и плоскость треугольника образуют двугранный угол, линейным углом которого являются два перпендикуляра к его ребру в точке С.
Угол АСВ - прямой, ⇒АС- перпендикуляр в плоскости треугольника к линии пересечения плоскостей, НС - перпендикуляр, проведенный в проведенной плоскости к той же линии.
Угол АСН =60°
АН - перпендикуляр к плоскости, НВ - проекция гипотенузы АВ на плоскость.
Угол АВН - искомый.
В равнобедренном прямоугольном треугольнике острые углы равны 45°.
Примем катеты ∆ АВС равными а. Тогда гипотенуза
АВ=а:sin 45°=a√2
АН=а•sin60°=a√3/2
sinАВН=АН:АВ=a√3/2):a√2=0,61237
Это синус угла ≈37,76°
Объяснение: