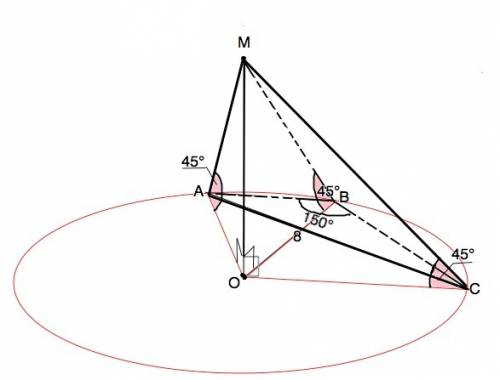
Обозначим основание пирамиды АВС, угол АВС=150°, высота пирамиды МО.
Боковые ребра наклонены к основанию под одинаковым углом, значит, их проекции равны между собой и равны радиусу описанной около основания окружности.
Треугольник АВС - тупоугольный. Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Так как угол наклона ребер равен 45°, то высота пирамиды является катетом равнобедренного треугольника и равна радиусу описанной окружности.
По т.синусов 2R=АС:sinАВС=
⇒ R=8 см
Высота МО пирамиды равна R=8 см
Пусть BH=y, тогда HC=y+9;
BT=(BH+HC)/2=(2y+9)/2 (KT-средняя линия), HT=BT-BH=(2y+9)/2-y=4,5(см).
Так как KT - средняя линия треугольника ABC, то MT ║ AC, то есть ∆MHT~∆AHC
(это можно обосновать равенством соответственных углов при параллельных прямых), коэфф.подобия k=MT/AC=5x/14x=5/14 =>
HT/HC=5/14 <=> 4,5/(y+9)=5/14. Решая это уравнение, получим,что y=BH=3,6 (см),
HC=y+9=12,6 (см), BC=BH+HC=3,6+12,6=16,2(см).
ответ: 16,2.