1)двумя катетами:
а)а=20,b=21
гипотенуза по теореме Пифагора
с=корень(a^2+b^2)=корень(20^2+21^2) = корень(841) =29
Неизвестные острые углы
cos a =a/c =20/29
a = arccos(20/29) = 46,4 градуса
y =90-a =90-46,4 =43,6
2)гипотенузой и катетом:
а)с=17,а=15
Найдем второй катет
b =корень(с^2-a^2) =корень(17^2-15^2) = корень(64) =8
Неизвестные острые углы
cos a =a/c =15/17
a = arccos(15/17) = 28,1 градуса
y =90-a =90-28,1 =61,9
3)гипотенузой и острым углом:
а)с=8,угол A=70 градусов
4)катетом и прилеглым углом:
а)а=12,угол А= 32 гра
Гипотенуза
с = a/cos70 = 12/cos70 = 35,1
другой катет
b = a*tg70=12*tg70 = 33
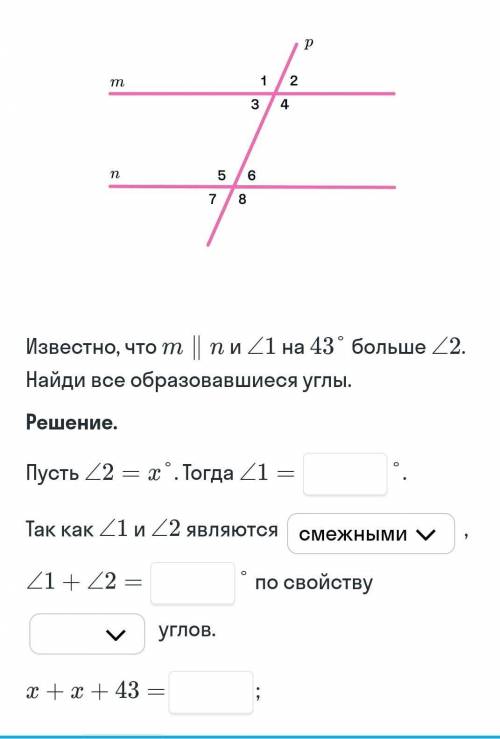
∠2=∠3=∠6=∠7=68,5°
∠1=∠4=∠5=∠8=111,5°
Объяснение:
Пусть ∠2=х°. Тогда ∠1= х°+43°.
Так как ∠1 и ∠2 являются смежными,
∠1+∠2=180° по свойству
смежных углов.
х+х+43°=180°
2х=137°
х=68,5°
∠2=68,5°, ∠1=68,5°+43°=111,5°.
Найдём остальные углы, воспользовавшись свойствами:
Вертикальные углы равны.Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны.Если две параллельные прямые пересечены третьей прямой, то соответственные углы равны.∠3=∠2=68,5° - как вертикальные
∠6=∠3=68,5° - как внутренние накрест лежащие углы образованные при пересечении параллельных прямых m и n секущей p.
∠7=∠3=68,5° - как соответственные углы образованные при пересечении параллельных прямых m и n секущей p.
Итак, ∠2=∠3=∠6=∠7=68,5°
∠4=∠1= 111,5° - как вертикальные
∠5=∠4=111,5° - как внутренние накрест лежащие углы образованные при пересечении параллельных прямых m и n секущей p.
∠8=∠4=111,5° - как соответственные углы образованные при пересечении параллельных прямых m и n секущей p.
Итак, ∠1=∠4=∠5=∠8=111,5°