Сделаем иллюстрацию. Примем, что О находится внутри треугольника.
Тогда ОА, ОВ и ОС - радиусы окружности. Раз ОВС равно 55, а ОВ=ОС, то треугольник ОВС равнобедренный и угол ОСВ тоже 55. Значит угол ВОС = 180-55-55=70
Теперь обозначим оставшиеся углы: АВО=ВАО=х, АСО=САО=у, АОВ=k, АОС=m. Составим систему уравнений:
1) 70+k+m=180 - для углов вокруг точки О
2) 2*55+2х+2у=180 - сумма углов треугольника АВС
3) k+2х=180 - сумма углов треугольника АВО
4) m+2у=180 - сумма углов треугольника АСО
Решаем систему:
Из (3): k=180-2x
Из (4): m=180-2у
Подставляя в (1): 70+180-2х+180-2у=180
2х+2у=70
Записываем (2): 2х+2у=70
Получились тождественно равные уравнения. Отсюда 2(х+у)=70, (х+у)=35
Посмотрим на рисунок - искомый нами угол и равен х+у. Значит, он равен 35 градусов
Насчёт решения для случая, когда О лежит вне окружности - не уверен, а проверять несколько лень
Так как не уточнено, как именно располагается угол 30 градусов относительно катета в 24 см, то возможно два варианта решения. Они различаются только цифрами, а суть одна.
Прямоугольный треугольник в основании. Один катет равен 24. Прилежащий угол равен 30 градусов. Найдем гипотенузу:
cos30 = 24/гипотенузу.
гипотенуза =  =
= 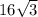 .
.
второй катет по теореме Пифагора будет равен:
катет2 = 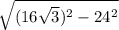 =
= 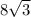 .
.
площадь прямоугольного треугольника в основании:
S(тр) = 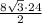 =
= 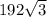
ТАких треугольников в призме 2.
Сама призма - прямая, значит грани перпендикулярны оснвоанию. Большая боковая грань будет опираться на гипотенузу. Ее диагональ находится к плоскости основания под углом 45 градусов. Треугольник образованный высотой призмы, этой диагональю и гипотенузой будет прямоугольным и равнобедренным. (один угол 90, на два дргуих остается 90, Раз один из них равен 45, то и второй тоже будет 45). Из всего этого следует, что высота призмы численно арвна гипотенузе - 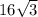 .
.
Находим площадь грани, опирающей на гипотенузу:
этот прямоугольник = 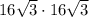 = 768.
= 768.
площадь грани, опирающейся на катет 24 см:
S = 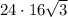 =
= 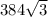
площадь грани, опирающейся на катет 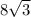 :
:
S = 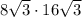 = 384.
= 384.
Теперь суммируем все площади и получаем полную боковую поверхность призмы:
S(полн) = 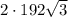 + 768 +
+ 768 + 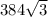 + 384 =
+ 384 = 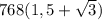
Угол 30 градусов в треугольнике основания является противолежащим относительно катета 24 см.
Тогда гипотенуза вдвое больше катета:
гипотенуза = 24*2 = 48.
второй катет =  =
= 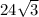 .
.
Так как треугольник в основании приумиды равен верхнему, то можно сразу найти их суммарную площадь (площадь одного треугольника = произведению катетов, деленному на2, а их сумма - это все равно, что помножить площадь одного треугольника на 2, то есть 2 сокращается).
S(обоих тр) = 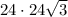 =
= 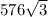
Высота призмы = 48.
Площадь прямоугольника, опирающегося на гипотенузу:
S = (48*48) = 2304.
площадь прямоугольника, опирающегося на катет 24 см:
S = 24*48 = 1152
площадь прямоугольника, опирающегося на второй катет:
S = 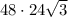 =
= 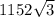
S(общая) = 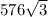 + 2304 + 1152 +
+ 2304 + 1152 + 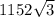 =
= 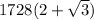
Полные выкладки делать некогда, поэтому советую числа перепроверить, потому как решала быстро.
очевидно угол B раен 90 градусов
Квадрат высоты прямоугольного треугольника, проведенной к гипотенузе равен произведению проекций катетов
поэтому
BK^2=AK*KC
12^2=6*AK
AK=144\6=24
AC=AK+KC=6+24=30
Квадрат катета равен произведению гипотенузы на его проекцию на гипотенузу, поэтому
AB^2=AK*AC
AB^2=24*30=720
AB=корень(720)=12* корень(5)
По определению cos A=AB\AC
cos A=12* корень(5)\30=2\5*корень(5)
ответ:30 см, 2\5*корень(5)