Построение сводится к проведению перпендикуляра из точки к прямой.
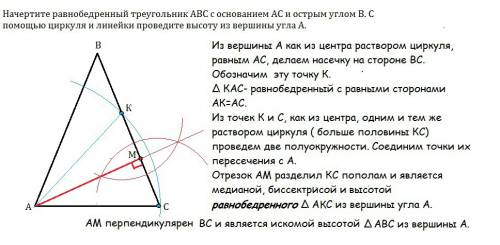
Из вершины А, как из центра, раствором циркуля, равным АС, делаем насечку на стороне ВС. Обозначим эту точку К.
∆ КАС- равнобедренный с равными сторонами АК=АС.
Разделив КС пополам, получим точку М, в которой медиана ∆ КАС пересекается с основанием КС. Т.к. в равнобедренном треугольнике медиана=биссектриса=высота, отрезок АМ будет искомой высотой.
Для этого из точек К и С, как из центра, одним и тем же раствором циркуля ( больше половины КС) проведем две полуокружности. Соединим точки их пересечения с А.
Отрезок АМ разделил КС пополам и является искомой высотой ∆ АВС из вершины угла А.
Пусть дан треугольник АВС, в котором АВ=ВС.
Основание треугольника АС равно 20 см.
Медиану из вершины В рассматривать не будем - она не может делить треугольник на два с разными периметрами.
Медианы из А и С делят исходный треугольник одинаково.
Поэтому в принципе это одно и то же решение.
Проведем медиану АМ из А к ВС.
Примем сторону АВ=2х см, тогда
медиана АМ делит ВС на две части по х см каждая.
Р (АВМ)= АВ+ВМ+АМ=2х+х+АМ=3х+АМ
Р(АСМ)= АС+СМ+АМ=20+х+АМ
Вариант1)
Р(АВМ)-Р(АСМ)=6 см
Тогда
3х+АМ-(20+х+АМ)=6
2х-20=6
2х=26 см
2х=АВ=ВС=26 см
Вариант 2)
Р(АСМ)-Р(АВМ)=6
20+х+АМ-(3х+АМ)=6
2х=АВ=ВС=14 см