***
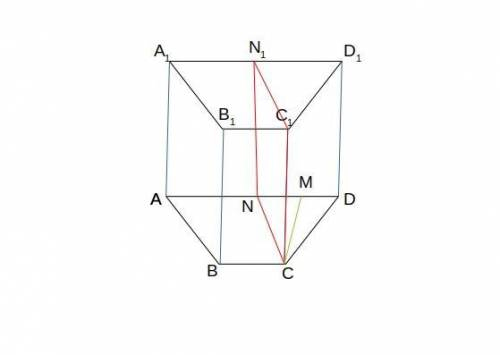
CNN1C1 - прямоугольник
сначала найдем площадь осн.
и поскольку основание призмы у нас трапеция
значит находим площадь трапеции ABCD
площадь трапеции равна произведению полусуммы ее оснований на высоту:
S = ((AD + BC) / 2) · СМ
(где высота трапеции — это перпендикуляр, проведенный из любой точки одного из оснований к прямой,
содержащей другое основание)
пусть ВС - х
АD - 6х
СN - 6х
S (осн.) = (BC + AD) · CM = (6х + х )/ 2 · 6х = 7х / 2 ·6х = 7х · 3х = 21х²
СС₁ = V / S (осн.) = 672 / 21х²
8 = 672 / 21x²
x² = 672 / ( 8 · 21)
x² = 672 / 168
x² = 4
=>
x = √4 = 2 см
ВС = х = 2
АD = 6х = 6 · 2 = 12 = CN
CN║AB
CN = AB
=>
из треугольника СND
треугольник - равнобедренный
CN = CD
=>
CM и медиана , и высота, и биссектриса
(свойства равнобедренного треугольника)
NM = ND = (AD - BC) / 2 = (12-2) /2 = 10/2 = 5 см
∠М = 90°
=>
по теореме Пифагора
сумма квадратов длин катетов равна квадрату длины гипотенузы
т.е.
c² = a² + b²
NC² = NM² + MC²
NC² = (5)² + 12)²
NC = √((5)² + 12)²)
NC = √(25 + 144)
NC= √169
NC = 13 см
поскольку CNN1C1 - прямоугольник
а для того чтобы найти площадь прямоугольника, надо его длину умножить на ширину
=>
S(CNN1C1) = 8 · 13 = 104 см²
ответ: 104 см²
Объяснение:
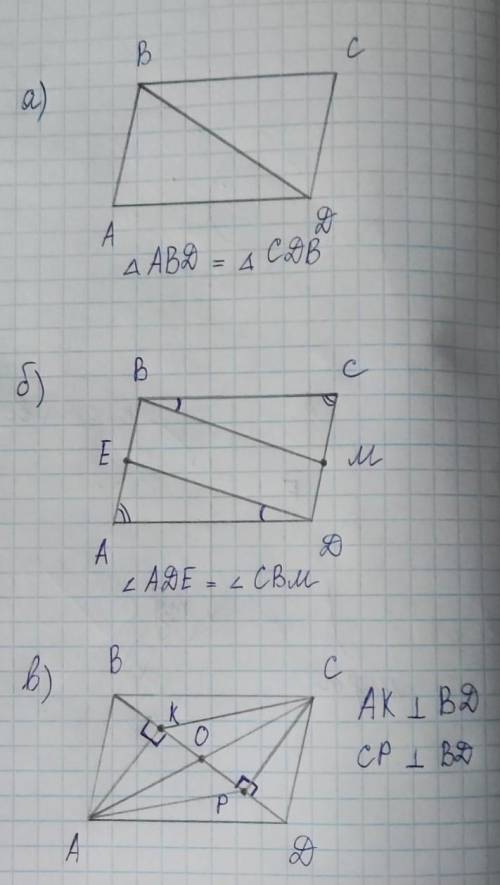
а) Из равенства треугольников имеем: AB = CD и AD = BC. Это значит, что стороны четырехугольника попарно равны, поэтому он и является параллелограммом.
б) AD = BC как стороны параллелограмма, <ADE = <CBM по условию, а <А = <С как противоположные углы параллелограмма, это значит, что ∆CMB = ∆AED. Из этого следует, что ED = BM. AE = CM (из равенства треугольников), значит EB = DM.
Из этого следует, что четырехугольник BEDM - параллелограмм.
в) Дополнительно проведем диагональ AC, которая является диагональю и для четырехугольника AKCP. AO = OC и BO = OD по свойству параллелограмма ABCD. <CPD = <AKB = 90°. CD = AB по свойству параллелограмма, AK = CP как перпендикуляры. Из вышеперечисленного следует, что ∆CPD = ∆AKB. Из равенства треугольников: BK = PD. KO = OB - BK, PO = OD - DP, поскольку OD = OB, а DP = BK, то PO = OB - BK, следовательно OK = OP. Диагонали четырехугольника AKCP делятся точкой пересечения пополам, поэтому AKCP - параллелограмм.
АВ=6см т.к.6:А1В1=3, 6:2= 3
АС=12см.т.к. 12:4=3
ВС=9т.к.9:3=З