Обозначим пирамиду МАВС.
Боковые ребра пирамиды наклонены под одинаковым (45°) углом к плоскости основания.
Значит, их проекции равны радиусу описанной окружности правильного треугольника, а вершина пирамиды проецируется в центр О ее основания.
Боковые ребра с высотой пирамиды образуют равнобедренный прямоугольный треугольник .
В ∆ МАО угол МАО= 45° (по условию). Поэтому высота МО пирамиды равна радиусу АО описанной окружности.
Радиус описанной окружности находят по формуле R=а/√3
R=АО=12:√3=12√3:3=4√3
МО=АО=4√3

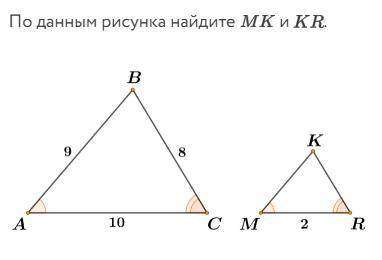
ответ: 1.8; 1.6
Объяснение:
Подобные треугольники => все стороны относятся соот-но с одинаковым отношением.
10/2 = 5. Далее составляем уравнения:
9/МК = 5
МК = 9/5 = 1,8
8/KR = 5
KR = 8/5 = 1.6