К такому заданию должен быть рисунок, так как квадраты могут быть расположены по-разному.
В Интернете такая задача встречается с двумя вариантами рисунков.
1. Так как квадраты не имеют оющих сторон, находим периметр одного квадрата:
1) 3960 : 5 = 792 см
2) 792 : 4 = 198 см - сторона квадрата
3) 198 · 198 = 39204 см² - площадь одного квадрата
4) 39204 · 5 = 196020 см² - площадь двора
1 м² = 10000 см²
196020 см² : 10000 = 19,602 м²
2. Так как квадраты имеют общие стороны, периметр состоит из 12 отрезков, равных стороне квадрата.
1) 3960 : 12 = 330 см - сторона квадрта
2) 330 · 330 = 108900 см² - площадь одного квадрата
3) 108900 · 5 = 544500 см² - площадь двора
544500 см² : 10000 = 54,45 м²
Решение:
1) Найдем объем отсеченной части пирамиды.
Так как плоскость сечения находится на расстоянии 3 см от вершины пирамиды, ее высота равна 3 см.
Объем пирамиды равен произведению 1/3 на высоту и на площадь основания.
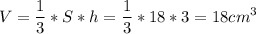
2) Плоскоcть сечения параллельна основанию пирамиды, поэтому пирамиды подобны.
Объемы подобных фигур относятся как их коэффициенты подобия в кубе.
Найдем коэффициент подобия:
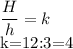
3) Значит отношение объемов фигур будет равно 4³=64
Найдем объем большой пирамиды
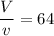
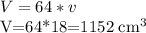
ответ Объем пирамиды 1152 см³
Пусть АВС - прямоугольный, а АВ - гипотенуза. Биссектрисы AD и ВЕ пересекаются в точке К. Биссектриса делит угол пополам. Сумма острых углов треугольника равна 90 градусов, поэтому сумма их половин - 45 градусов. Следовательно в треугольнике АКВ угол при вершине К равен 180 - 45 = 135 градусов, а острый угол при пересечении биссектрис 180 - 135 = 45 градусов.