Объяснение:
Дано:
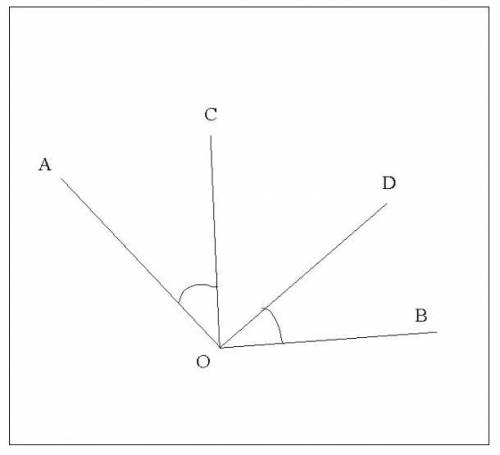
<AOB и <COD
<COD внутри <AOB
AO ┴ OD; CO ┴ OB;
<AOB - <COD = 90°
Найти: <AOB и <COD.
Решение
Т.к . AO ┴ OD; CO ┴ OB,
то <AOD = 90; <COB = 90°.
<COD = <AOD - <AOC
<COD = <COB - <DOB
<COD = 90° - <AOC
<COD = 90° - <DOB
Получим
<AOC = 90° - <COD
<DOB = 90° - <COD
Следовательно <AOC = <DOB
2) По условию: <AOB - <COD = 90°
Но если от всего угла <AOB отнять <COD, то останутся два равных угла <AOC и <DOB, значит, это их сумма равна 90°.
<AOC + <DOB = 90° =>
<AOC = <DOB = 90°/2 = 45°
3) <COD = 90° - <DOB
<COD = 90° - 45°=45°
4) <AOB = <AOC + <DOB + <DOB
<AOB = 45° + 45° + 45° = 135°
ответ: <AOB - 135°; <COD =45°.
обозначим стороны этого треугольника a, b, c.
каждая боковая грань призмы - параллелограмм, для оторого известна одна из сторон - боковое ребро призмы, 5 см.
площадь двух граней дана.
S_1 = a*5 = 20
a = 4 см
S_2 = b*5 = 20
b = 4 см
Теперь известны две стороны сечения по 4 см и угол между ними в 60 градусов.
треугольник сечения равнобедренный с углом при вершине 60°
Угол при основании
(180 - 60)/2 = 120/2 = 60°
Т.е. треугольник равносторонний
c = 4 см
площадь третьей грани
S_3 = 4*5 = 20 см^2
Полная боковая поверхность
3*20 = 60 см^2