Нехай маємо прямокутний трикутник ABC (∠C=90), AL – бісектриса, яка проведена до сторони BC, тоді ∠ALC=70 градусів (за умовою).
Побудуємо рисунок трикутника та бісектриси в ньому

У прямокутному ΔALC (∠ACL=90), за теоремою про суму кутів трикутника, знайдемо ∠CAL:
∠CAL=180-∠ACL-∠ALC=180-90-70=20.
За означенням бісектриси AL в трикутнику ΔABC отримаємо:
∠A=2•∠CAL=2•20=40.
У прямокутному ΔABC (∠C=90), за теоремою про суму кутів трикутника, знайдемо ∠B:
∠B=180-∠C-∠A =180-90-40=50
Отже, ∠A=40 – менший гострий кут ΔABC.
Відповідь: 40 градусів.
Приклади на кути трикутника, та й загалом на геометричні фігури слід розв'язувати з побудови допоміжного рисунку (неважна якість, головне намалювати та позначити задані величини); далі виписування, що задано та самого обчислення шуканих величин.
Як тільки навчитеся будувати геометрію, все решта прийде в процесі розв'язування.
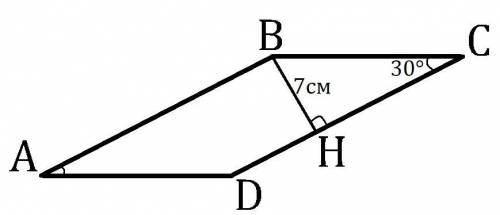
BH = 7см, как перпендикуляр к прямой CD.
ΔBHC - прямоугольный (∠BHC=90°), а ∠HCB=30°, поэтому BC=2·BH=7см·2=14см т.к. BH - катет лежащий напротив угла в 30°.
AD = BC = 14см, как противоположные стороны параллелограмма.
Так же AB = DC = (P-AD-BC):2 = (60-14-14):2 = 30-14 = 16см
∠BAD = ∠BCD = 30°, как противоположный углы параллелограмма.
Так же ∠ABC = ∠ADC = (360°-∠BAD-∠BCD):2 = (360°-30°-30°):2 = 180°-30° = 150°.
AB = 16см; BC = 14см; DC = 16см; AD = 14см;
∠BAD = 30°; ∠ABC = 150°; ∠BCD = 30°; ∠ADC = 150°.