Пусть О — точка пересечения высоты BD и биссектрисы AE.
AO : OE = 23 : 13, BD = 12 см. По теореме Менелая для треугольника АЕС имеем . Поскольку треугольник ABC равнобедренный, то BD является биссектрисой и медианой, т.е. AD = DC, тогда (1).
По свойству биссектрисы: .
По теореме Пифагора из прямоугольного треугольника BDC:
Подставляем в равенство (1), получим уравнение относительно АС.
Решаете как иррациональное уравнение, возводите два раза обе части уравнения и вы должны придти к биквадратному уравнению , получите см.
1) a+b = 180 градусов, b = a-40 градусов, a+(a-40) = 180, 2a = 180+40 = 220, a = 220/2 = 110, b=110 - 40 = 70. ответ. 110 градусов. 2) Если хорда перпендикулярна диаметру, то она сама делится пополам этим диаметром (докажи!). Таким образом отрезки, на которые делится хорда диаметром это 15 см и 15 см. А отрезки, на которые делится диаметр хордой будут, t и (9t). По известной теореме для пересекающихся хорд имеем. 15*15 = t*9t, 15^2 = 9(t^2) = (3t)^2, 3t = 15; t = 15/3 = 5 см. D = t + 9t = 10t = 10*5 = 50 см. ответ. 50 см.
Пусть О — точка пересечения высоты BD и биссектрисы AE.
AO : OE = 23 : 13, BD = 12 см. По теореме Менелая для треугольника АЕС имеем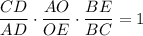
. Поскольку треугольник ABC равнобедренный, то BD является биссектрисой и медианой, т.е. AD = DC, тогда 
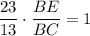(1).
По свойству биссектрисы: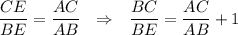
.
По теореме Пифагора из прямоугольного треугольника BDC:
Подставляем в равенство (1), получим уравнение относительно АС.
Решаете как иррациональное уравнение, возводите два раза обе части уравнения и вы должны придти к биквадратному уравнению , получите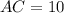
см.
Площадь треугольника: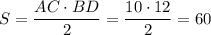
см²
ответ: 60 см².