Пусть трапеция АCВD, проведем через С прямую II BD до пересечения с продолжением AD в точке Е. Треугольник АВЕ имеет ту же площадь, что и трапеция, потому что его основание АЕ = АD + ВС, а высота АВЕ и ABCD - это расстояние от точки С до АВ (то есть высота общая).
Таким образом, нам надо найти площадь треугольника (АВЕ) со сторонами 12, 16 и 20. Легко видеть, что это египетский треугольник, подобный (3,4,5), то есть он прямоугольный. Его площадь равна 12*16/2 = 96
Мы так походя доказали, что диагонали взаимно перпендикулярны. Если не понятно про "египетский треугольник", проверьте, что 12^2 + 16^2 = 20^2.
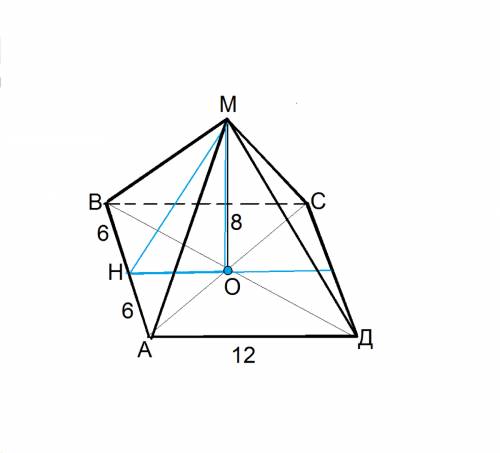
Высота правильной четырехугольной пирамиды равна 8 см, сторона ее основания 12 см. Вычислите длину бокового ребра пирамиды и площадь боковой поверхности пирамиды.
В основании пирамиды квадрат, она правильная - значит, основание ее высоты находится в точке пересечения диагоналей квадрата, а все грани - равные равнобедренные треугольники.
Ребро МД=√(ОД²+ОМ²)
ОМ=8 см, ОД - половина диагонали квадрата и равно 6√2
МД=√(72+64)=√136=√(4•34)=2√34 - это длина бокового ребра.
Площадь боковой поверхности равна произведению апофемы ( высоты боковой грани) на половину периметра основания.
S=MH*4*АД:2=МН*2АД
МН из треугольника МОН ( египетского!) равно 10 ( можно проверить по т. Пифагора)
Sбок=10*24=240 см ²
_________
[email protected]
R=8cm/2=4cm
h=6cm
V=4*4*6π=144π cm³