Даны координаты точек A(1;4), B(1;1) , C(4;7).
Уравнение прямой, включающей сторону ВС:
Вектор BC : (4-1=3; 7-1=6) = (3; 6).
(x - 1)/3 = (у - 1)/6, после сокращения знаменателей на 2, получаем:
(x - 1)/1 = (у - 1)/2 это каноническое уравнение стороны ВС.
Или 2х - 2 = у - 1 или 2х - у - 1 = 0 общее уравнение.
у = 2х - 1 с угловым коэффициентом. к(ВС) = 2.
Угловой коэффициент перпендикуляра АН к стороне ВС равен:
к(АН) = -1/к(ВС) = -1/2.
Уравнение АН: у = (-1/2)х + в. Для определения параметра в подставим координаты точки А: 4 = (-1/2)*1 + в, отсюда в = 4 + (1/2) = 9/2.
Уравнение АН: у = (-1/2)х + (9/2).
Координаты точки Н находим как точки пересечения прямых АН и ВС.
(-1/2)х + (9/2) = 2х - 1,
(5/2)х = (11/2), отсюда находим х(Н) = 11/5 = 2,2.
у(Н) = 2*(11/5)-1 = 17/5 = 3,4.
ответ: Н(2,2; 3,4).
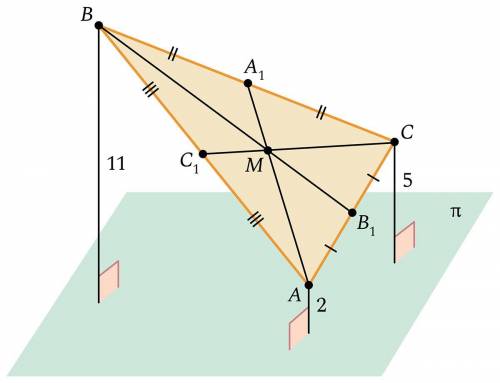
МД₁=6
Объяснение:
Искомым расстоянием от точки пересечения медиан М, до плоскости π является отрезок МД₁.
Обозначим высоты от стороны АС к плоскости π: В₁К, АЕ, СЕ₁. Соединим точки Е и Е₁. Получим трапецию ЕАСЕ₁. В₁К || АЕ || СЕ, так как они перпендикулярны плоскости π. По теореме Фалеса если параллельные прямые, пересекая стороны угла отсекают равные отрезки на одной его стороне, то они отсекают равные отрезки и на второй стороне угла, поэтому если АВ₁=В₁С, то ЕК=КЕ₁. → В₁К – средняя линия трапеции ЕАСЕ₁.
В₁К=(ЕА+Е₁С)÷2=(2+5)÷2=7÷2=3,5
Проведём перпендикуляры В₁Н и КК₁ к стороне ВК₁, получили трапецию В₁КК₁В.
В₁Н делит ВК₁, что К₁Н=В₁К=3,5, тогда ВН=11–3,5=7,5.
Рассмотрим ∆ВВ₁Н, он прямоугольный, ВН и В₁Н – катеты, ВВ₁ – гипотенуза. Медианы треугольника, пересекаясь, точкой пересечения делятся на отрезки в отношении 2 : 1, начиная от вершины треугольника, поэтому ВМ : МВ₁=2 : 1 и по теореме Фалеса ДН : В₁Д=2 : 1. МД || ВН, и МД отсекает от ∆ВВ₁Н подобный ему ∆МВ₁Д. Стороны ∆ВВ₁Н имеют 3 части (2+1=3), а стороны ∆МВ₁Д – одну часть. Пусть МД=х, запишем пропорцию:
МД : ВН=1 : 3
Произведение крайних членов пропорции равно произведению средних:
МД•3=ВН•1
3х=7,5•1
3х=7,5
х=7,5÷3
х=2,5
ДД₁=В₁К=НК₁=3,5
МД₁=МД+ДД₁=2,5+3,5=6