Пусть точка P(x₀, y₀) удовлетворяет системе уравнений. Возьмём квадратный корень из левой и правой части каждого уравнения:
Первое уравнение задаёт расстояние от точки P(x₀, y₀) до точки A(-4, -3), равное трём. Второе уравнение задаёт расстояние от точки P(x₀, y₀) до точки B(-1, 1), равное двум.
Заметим, что расстояние между точками A(-4, -3) и B(-1, 1) равно . Расстояние между данными точками равно сумме расстояний между точками P(x₀, y₀) и A(-4, -3) и между точками P(x₀, y₀) и B(-1, 1) (AB (5) = AP (3) + PB (2)). Значит, точка P(x₀, y₀) находится на отрезке между точками A(-4, -3) и B(-1, 1) и делит его в отношении 3 : 2, считая от точки A(-4, -3). Тогда справедливо
Поскольку точка A находится не в начале координат, выполнив параллельный перенос на вектор , мы получим координаты точки P(x₀, y₀): .
Дано: АВСD - равнобокая трапеция, АВ=СD= 6 см, МN- средняя линий, МО= 2 см; ОN=5 см. Найти: ∠ВАD, ∠АВС Решение. ΔАВС. ОМ- средняя линия, равна 2 см, значит ВС=4 см., средняя линия в 2 раза меньше ВС. ΔАСD. ОN- средняя линия равна 5 см. значит АD= 10 см.Построим СК║АВ. АВСК - параллелограмм, противоположные стороны параллельны и равны: АК=ВС=4 см.СК=АВ=6 см. ΔСDК равнобедренный: СК=СD= 6 см. Построим СН⊥АD, тогда КD=АD-АК=10-4=6 см. Но СН также является медианой в равнобедренном ΔКСD, значит КН=НD=6/2=3 см. ΔСDН. cosD=HD/CD=3/6=0,5. ∠НDС=60°. ∠ВАD=СDА=60°. ∠АВС=∠ВСD=180-60=120°. ответ: 60°; 120°.
(-2,2; -0,6)
Объяснение:
Пусть точка P(x₀, y₀) удовлетворяет системе уравнений. Возьмём квадратный корень из левой и правой части каждого уравнения:
Первое уравнение задаёт расстояние от точки P(x₀, y₀) до точки A(-4, -3), равное трём. Второе уравнение задаёт расстояние от точки P(x₀, y₀) до точки B(-1, 1), равное двум.
Заметим, что расстояние между точками A(-4, -3) и B(-1, 1) равно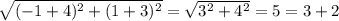
. Расстояние между данными точками равно сумме расстояний между точками P(x₀, y₀) и A(-4, -3) и между точками P(x₀, y₀) и B(-1, 1) (AB (5) = AP (3) + PB (2)). Значит, точка P(x₀, y₀) находится на отрезке между точками A(-4, -3) и B(-1, 1) и делит его в отношении 3 : 2, считая от точки A(-4, -3). Тогда справедливо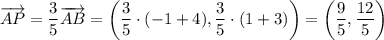 
Поскольку точка A находится не в начале координат, выполнив параллельный перенос на вектор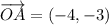
, мы получим координаты точки P(x₀, y₀): 
.
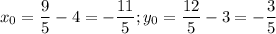Решением системы является точка (-2,2; -0,6).