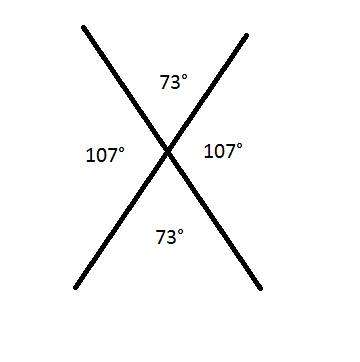
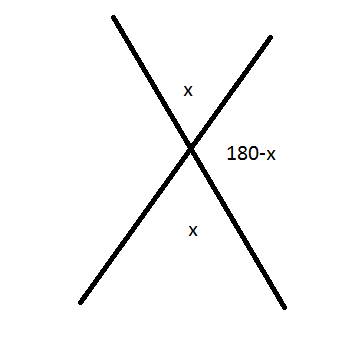

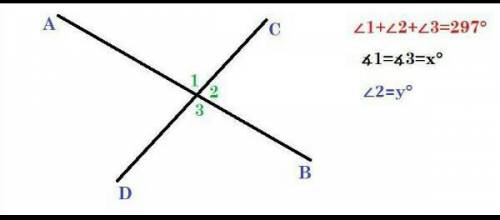
Дано:
AB ∩ CD
∠1 + ∠2 + ∠3 = 297˚.
Найти:
Все неразвёрнутые углы.
__________________________________
Мы знаем точно, что два угла из трёх - вертикальные, а значит между собой они равны.
Пусть x° равны ∠1 и ∠3, тогда ∠2 равен y°. Сумма смежных углов равна 180°, а сумма трёх данных углов - 297°.
Составляем систему уравнений:
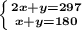
Работа с системой уравнения:
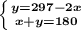
__________________________________
x + (297 - 2x) = 180
x + 297 - 2x = 180
- x = - 117
x = 117
117˚ - ∠1.
НО: Так как прямые образуют вертикальные углы ⇒ ∠1 = ∠3, по свойству.
=> ∠3 = ∠4, тоже по свойству.
∠3 = 297 - (117 + 117) = 63° - ∠3 и ∠4.
Сумма всех 4 углов равна 360°.
ответ: 117˚; 117˚; 63˚; 63˚.
1 решение: угол А= углу В= 52°; угол С равен 76°
2 решение: угол А= углу В = 68°; угол С равен 44°
Объяснение:
решение 1
угол А и угол В равны ( по св-ву р/б треугольника следует, что углы, лежащие у его основания равны) => ни один из этих углов не может быть больше или меньше друг друга => угол С будет иметь разность с углами А и В, т. е. он может быть больше на 24° и меньше (получается, что задача имеет два решения, тк что угол А или В могут быть больше угла С, что он может быть больше угла А или В).по сумме углов трекгольника следует, что:180°-2x=x+24° (за х мы обозначили равные углы А и В, а 24° это то, насколько угол С больше углов А и В)180°-3х=24°х=(180°-24°):3 = 156°:3=52° х+24°=52°+24°=76° (это угол С в том решении, когда он больше А и В на 24°)
решение 2
180-2x=x-24
180-3x=-24
=>3x= 180°+24°=204°=>x=204°:3=68°(это у нас будут углы А и В, тк во втором решени они будут на 24° больше, чем С)
по сумме углов т-ка:
180-(68+68)=180-136=44°( это у нас С)