
У трикутнику ABC, <А = <В = 75°. Знайдіть ВС, якщо площа дорівнює 36 см2 -------------------------------------------------
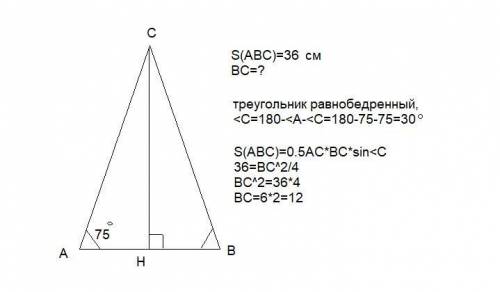
В треугольнике ABC , ∠А = ∠В = 75 °. Найдите BC, если площадь равна 36 см² . -------------------------------------------------
"Решение" : ∠C = 180° -( ∠А+∠В ) =180°- ( 75° + 75° ) =180°- 150°=30° .
Достаточно провести высоту AH ( AH ⊥ BC , H ∈[ BC] )
ΔAHC : AH = AC/2 (как катет против угла 30° ) ⇔ AH = BC/2
S=BC*AH /2 = (BC*BC/2 ) /2 = BC²/4 ⇔ BC² =4S ⇔ BC =2√S
BC =2√(36 см²) = 2*6 см =12 см .
ответ : 12 см .
рисунок Δ см приложения
Объяснение:
1
Рассмотрим тр-к АВС
По теореме Пифагора :
АВ=корень (АС^2+ВС^2)=
=корень (24^2+32^2)=корень 1600=40 мм
СD=AD=BD=AB:2=40:2=20 мм
Тр-к КСD:
По теореме Пифагора :
КD=корень (КС^2+СD^2)=
=корень (48^2+20^2)=корень 2704=
=52 мм
2
А) АК _|_ МК - НЕТ (т. к <МКА=60 градусов)
Б) тр-к АКС - прямоугольный - ДА(т. к <АКС=90 градусов)
В) тр-к МАК - равносторонний - ДА (т. к
КА=КМ, значит тр-к АКМ-равнобедренный, т. к <МКА=60 градусов <КАМ=<КМА=(180-<МКА)/2=
=(180-60)/2=60 градусов, значит тр-к
МАК- равносторонний
Г) МК_|_(АКС) - ДА
Д) тр-к МАС - прямоугольный - НЕТ
ответ : Б) ; В) ; Г)