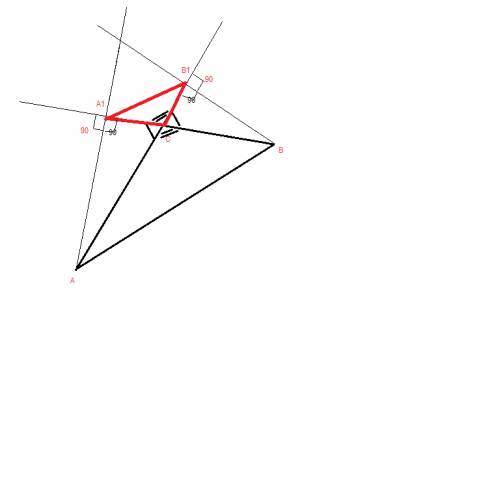
Доказать подобие треугольников А1СВ1 и АВС.
сделаем построение по условию
треугольники ACA1 и ВСВ1 - подобные по ПЕРВОМУ признаку подобия (по двум углам)
<AA1C=<BB1C=90 град
<ACA1=<BCB1 -вертикальные
следовательно , соответственные стороны относятся
СA1 / CB1 =CA / CB = k1 -коэффициент подобия для треугольников ACA1 и ВСВ1
отношение можно записать по-другому
СA1 / CA = CB1 / CB = k2 -коэффициент подобия для треугольников А1СВ1 и АВС.
т.е. треугольники А1СВ1 и АВС подобны по ВТОРОМУ признаку подобия
(если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны)
пропорциональные стороны СA1 / CA = CB1 / CB
<A1CB1 = <ACB --вертикальные
доказано подобие треугольников А1СВ1 и АВС.
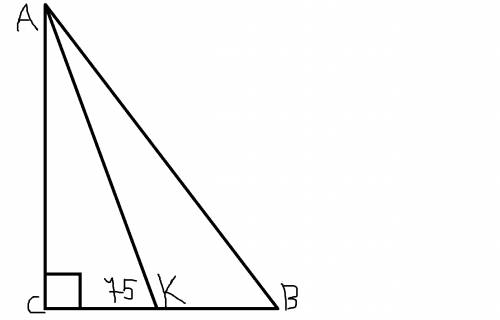
Дано:АВС-прямоугольный треугольник
угол АКС=75
угол С=90
угол А?
Решение:
угол САК=180-(75+90)=15
угол АКВ=180-75=105
угол КаБ=САК (т.к биссектриса делит пополам угол А)
угол В=180-(105+15)=60
и соответсвенно угол А=15+15=30
ответ:30 градусов
Я не знал какой именно угол тебе нужен поэтому нашел все))
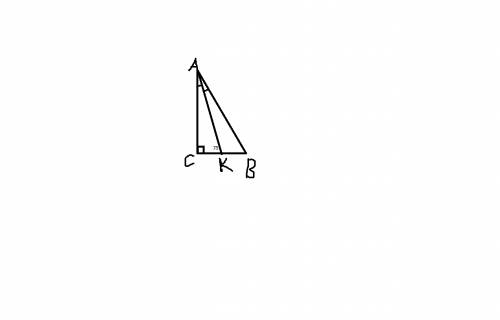
Углы при основании равнобокой трапеции равны, углы противоположные в сумме составляют 180°. Следовательно, указана сумма двух острых углов при нижнем основании.
2β = 360 - 2α
β = (360 - 2α)/2 = (360-92)/2 = 268/2 = 134°