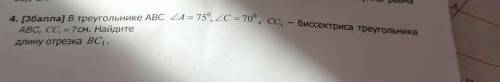
7
Объяснение:
Чертёж в прикреплённом файле.
1) Так как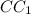 
- биссектриса ∠C, равного 70°, то ∠
= ∠
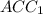= 0.5 * ∠C = 35°
2) Для треугольника ABC по теореме о сумме углов треугольника ∠B = 180° - ∠A - ∠C = 35°
3) Для треугольника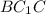 
имеем:
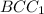∠ = 35° (п. 1)
∠B = 35° (п. 2)
Два угла треугольника равны, значит он равнобедренный,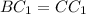 
По условию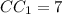 
⇒ 
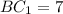
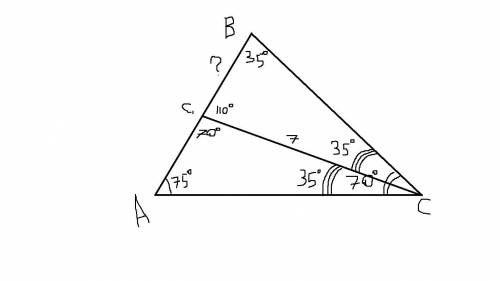
Дано: ∠А = ∠D = 60°, AB = CD = 12 см, AD = 18 см.
Найти: BC, MN (средняя линия)
Проведём высоты BH и CP. Рассмотрим треугольник ABH:
∠А = 60° по условию, ∠АВН = 90°; по теореме о сумме углов треугольника получаем: ∠АВН = 90° - 60° = 30°. АН = 0,5 АВ = 6 см, как катет прямоугольного треугольника, лежащий против угла в 30°. Так как трапеция ABCD - равнобедренная, то PD = AH = 6 см.
НР = AD - AH - PD = 18 - 12 = 6 см. BC = HP = 6 см, как противоположные стороны прямоугольника.
Средняя линяя трапеции равна полу сумме оснований ⇒ MN = (ВС + НР)/2 = (18 + 6)/2 = 12 см.
ответ: MN = 12 см, BC = 6 см.
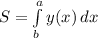(1)
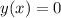
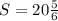
ответ: 7 см
Решение: сумма углов треуг =180 > 180-(70+75)= 35°
тк СС1 бисс, то угол ВСС1= 35° > треугол. ВСС1 равнобедренный и сторона СС1=ВС1=77см