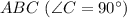 вписана окружность, касающаяся его сторон в точках
вписана окружность, касающаяся его сторон в точках 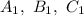 . Найти отношение площади треугольника
. Найти отношение площади треугольника 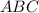 к площади треугольника
к площади треугольника 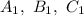 , если
, если 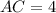 см,
см, 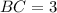 см.
см.По теореме Пифагора, AB²=BC²+AC²
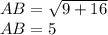
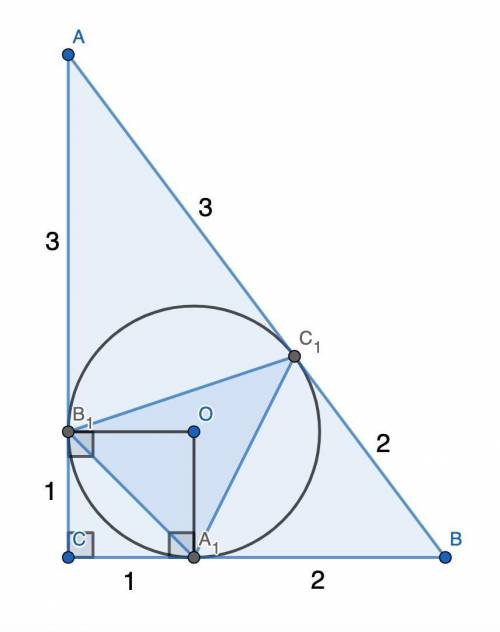
Прямоугольный треугольник точками касания вписанной окружности делится на значения как на фото.
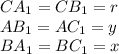
r – радиус вписанной окружности.
Радиус вписанной окружности в прямоугольный треугольник находится по формуле

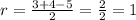
r=1
x=BC-r
x=3-1=2
y=AB-x
y=5-2=3
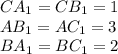
Площадь треугольник – половина произведения двух сторон и синуса угла между ними.
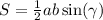
Площадь ΔABC:
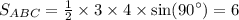
Площадь треугольника A1B1C1:
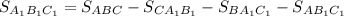
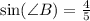
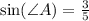
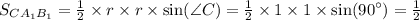

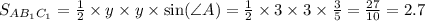
И теперь найдем площадь ΔA1B1C1:
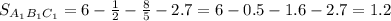
Отношение площади ΔABC на площадь ΔA1B1C1:
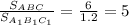
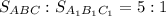
Дано: Решение:
∠AOB = 1/9 ∠BOC ∠AOB = ∠COD и ∠BOC = ∠DOA как
вертикальные углы при пересекающихся
Найти: ∠AOB; ∠BOC; прямых.
∠COD; ∠DOA Тогда: ∠AOB = ∠COD = х
∠BOC = ∠DOA = 9х
Сумма всех 4-х углов - 360°
2*(х + 9х) = 360
10х = 180
х = 18 9х = 162
∠AOB = ∠COD = 18°
∠BOC = ∠DOA = 162°
Может так ?
5
Объяснение:
Гипотенуза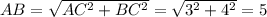 . Радиус вписанной в прямоугольный треугольник окружности
. Радиус вписанной в прямоугольный треугольник окружности 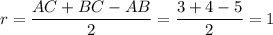 . Площадь
. Площадь 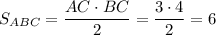 .
.
Рассмотрим четырёхугольник OA₁CB₁: ∠С = 90° по условию, ∠A₁ = ∠B₁ = 90° как углы между радиусом и касательной, тогда ∠O = 360° - ∠C - ∠A₁ - ∠B₁ = 360° - 3·90° = 90°. Значит, OA₁CB₁ — прямоугольник, но поскольку OA₁ = OB₁ = r, это квадрат. Тогда OA₁ = OB₁ = B₁C = A₁C = 1.
AC₁ = AB₁ как отрезки касательных, проведённых из одной точки. При этом AB₁ = AC - B₁C = 4 - 1 = 3, т. е. AC₁ = AB₁ = 3. Аналогично BC₁ = A₁B = BC - A₁C = 3 - 1 = 2.
Найдём площадь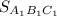 путём вычитания площадей
путём вычитания площадей 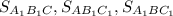 из площади
из площади 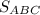 :
: