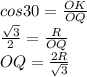
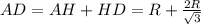
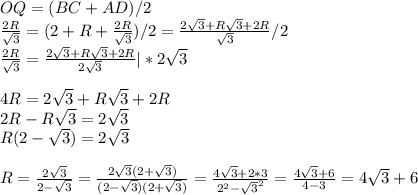
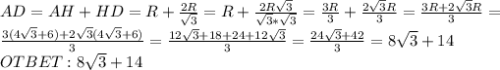
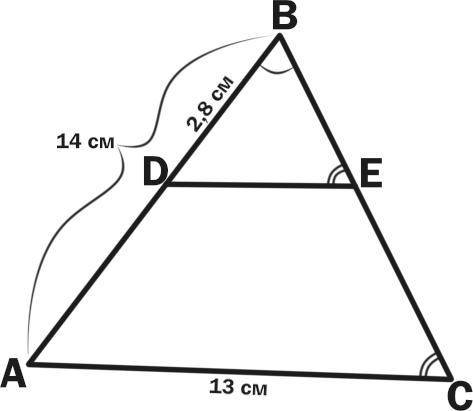
Дано :
ΔАВС.
D ∈ AB.
E ∈ BC.
DE ║ AC.
DB = 2,8 см.
АВ = 14 см.
АС = 13 см.
Найти :
ED = ?
Краткое -
∢BDE = ∢BАC, т. к. соответственные углы.
∢BЕD = ∢BCA, т. к. соответственные углы ⇒ ΔABС ∼ ΔDBЕ.
DE = 2,6 см.
Полное -
∠В - общий для ΔАВС и ΔDBЕ.
Рассмотрим соответственные ∠BED и ∠ВСА при пересечении параллельных прямых ED и АС секущей ЕС.
При пересечении двух параллельных прямых секущей соответственные углы равны.Тогда -
∠BED = ∠ВСА.
Следовательно, ΔАВС ~ ΔDBЕ по двум равным углам (первый признак подобия треугольников).
В подобных треугольниках против равных углов лежат сходственные стороны.Тогда пара сторон -
АВ и BD - сходственные стороны
АС и DE - сходственные стороны.
Отношения сходственных сторон подобных треугольников равны.То есть -
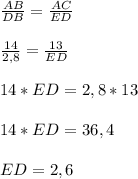
ED = 2,6 см.
2,6 см.
угол АСВ РАВЕН 74 ГРАДУСАМ
Объяснение: