4.Площадь треугольника АВС равна 6√3 см. АВ = 8 см, АС = 3 см. Найдите величину угла ВАС.

Question

Геометрия: 4.Площадь треугольника АВС равна 6√3 см. АВ = 8 см, АС = 3 см. Найдите величину угла ВАС.

Adelia742 · Accepted Answer

Дано: АВСД - трапеция, ВС=12 см, АД=18 см, АС- биссектриса угла А

Найти S трапеции

1) ВС||АД, АС - секущая. Значит ∠ВСА=∠САД как накрест лежащие.

2) ∠ВАС=∠САD , потому что АС- биссектриса.

∠ВСА=∠САД как накрест лежащие. (см. пункт 1)

Отсюда следует, что ∠ВАС=∠ВСА.

3) Рассмотрим треугольнике АВС. Он равнобедренный, так ка углы при основании равны.(∠А=∠С из пункта 2). Значит АВ=ВС=12 см

4) Рассмотрим ΔАВН. ВН- высота, АВ=12 см, АН=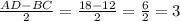 $\frac{AD-BC}{2} = \frac{18-12}{2} = \frac{6}{2} =3$ см. Этот треугольник прямоугольный, поэтому по теореме Пифагора найдём катет ВН

ВН= 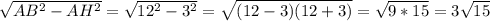$\sqrt{AB^2-AH^2}= \sqrt{12^2-3^2}=\sqrt{(12-3)(12+3)} = \sqrt{9*15}=3 \sqrt{15}$ см

5) Найдем площадь трапеции

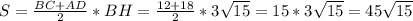$S= \frac{BC+AD}{2}*BH= \frac{12+18}{2}*3 \sqrt{15} =15*3 \sqrt{15} = 45 \sqrt{15}$ см²

Основания равнобокой трапеции равны 12 см и 18 см, а диагональ является биссектрисой её острого угла

MOGZ ответил