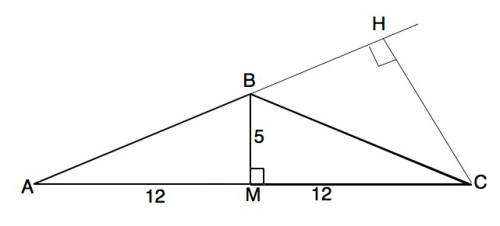
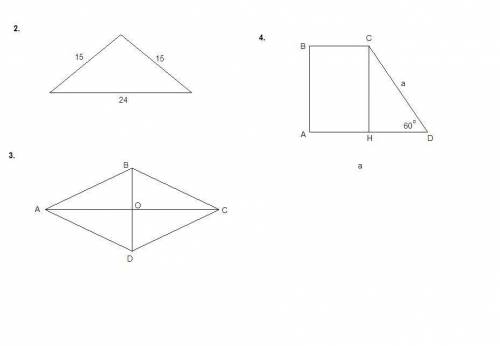
Медиана равнобедренного треугольника, проведенная к основанию, является и его высотой. АМ=МС=24^2=12 см, ВМ⊥АС. Из прямоугольного ∆ ВМС по т.Пифагора гипотенуза ВС=√(BM²+MC²)=13 см. Из прямоугольного ∆ ВМС синус угла при основании ВМ:ВС=5/13.
Проведем высоту СН к стороне АВ. Высота тупоугольного треугольника, проведенная из острого угла, проходит ВНЕ его и пересекает продолжение стороны. Треугольник АНС прямоугольный ( т.к.СН высота). АС - гипотенуза. Угол А=углу С ( ∆ АВС равнобедренный). Синус угла А=5/13. Искомая высота – катет СН=АС•sinA=24•5/13=9³/₁₃
Сфера задана уравнением x²+y²+z² -8y+4x+11=0
Найдите координаты центра и радиус сферы.
Решение.
x²+y²+z² -8y+4x+11=0 перегруппируем и добавим в каждую скобку сводный член для выделения полного квадрата
(x²+4х+4)-4+(y²-8у+16)-16+z²+11=0
(х+2)²-4+(у-4)²-16+z²+11=0
(х+2)²+(у-4)²+z²=16+4-11 или (х+2)²+(у-4)²+z²=9
(х+2)²+(у-4)²+z²=3². Тогда координаты центра сферы (-2;4;0) , R=3
Уравнение сферы (x – х₀)²+ (y – у₀)²+(z-z₀ )² = R² , где (х₀; у₀; z₀)-координаты центра, R- радиус