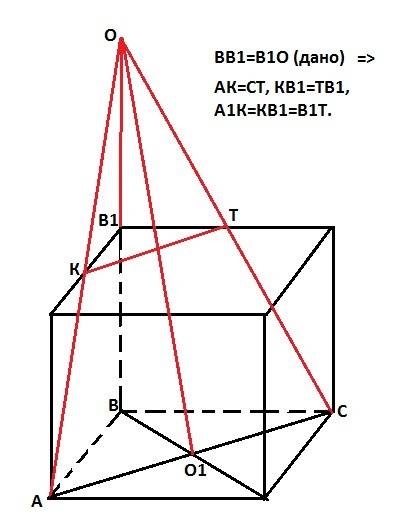
1. АВСD - квадрат. Диагонали квадрата взаимно перпендикулярны и точкой пересечения О1 делятся пополам. Следовательно, прямая ОО1 - перпендикулярна АС по теореме о трех перпендикулярах, так как ВО (перпендикулярная АС) - проекция наклонной ОО1. Тогда треугольник АОС - равнобедренный (ОО1 - высота, медиана и биссектриса), АО=ОС и КТ - его средняя линия (так как ВВ1=В1О - дано) => АК=ТС => четырехугольник АКТС - равнобедренная трапеция. Что и требовалось доказать.
2. Средняя линия трапеции - полусумма ее оснований. АС=2√2см (диагональ квадрата со стороной = 2см), а КТ=√2 (по Пифагору, так как треугольник КВ1Т - прямоугольный, равнобедренный, с катетами = 1). Тогда средняя линия трапеции равна 1,5*√2 см.
1. АВСD - квадрат. Диагонали квадрата взаимно перпендикулярны и точкой пересечения О1 делятся пополам. Следовательно, прямая ОО1 - перпендикулярна АС по теореме о трех перпендикулярах, так как ВО (перпендикулярная АС) - проекция наклонной ОО1. Тогда треугольник АОС - равнобедренный (ОО1 - высота, медиана и биссектриса), АО=ОС и КТ - его средняя линия (так как ВВ1=В1О - дано) => АК=ТС => четырехугольник АКТС - равнобедренная трапеция. Что и требовалось доказать.
2. Средняя линия трапеции - полусумма ее оснований. АС=2√2см (диагональ квадрата со стороной = 2см), а КТ=√2 (по Пифагору, так как треугольник КВ1Т - прямоугольный, равнобедренный, с катетами = 1). Тогда средняя линия трапеции равна 1,5*√2 см.

Стороны оснований равны 24 см и 8 см;
Высота = 15 см.
Найдем площадь полной поверхности.
1) Найдем площадь основания.
S осн = 24 см * 24 см + 8 см * 8 см = 24^2 см^2 + 8^2 см^2 = 576 см^2 + 64 см = 640 см^2.
2) Найдем ребро пирамиды по теореме Пифагора.
l^2 = h^2 + ((24 - 8)/2)^2 = 15^2 + ((24 - 8)/2)^2 = 15^2 + (16/2)^2 = 15^2 + 8^2 = 225 + 64 = 289 = 17^2;
Тогда: l = 17 см;
3) Найдем площадь боковой поверхности.
S бок = 4 * l * (a + b)/2 = 4 * 17 * (8 + 24)/2 = 2 * 17 * (8 + 24) = 34 * 32 = 1088 см^2.
4) Найдем площадь полной поверхности.
S полн.= S бок + S осн = 1088 см^2 + 640 см^2 = 1728 cм^2.