Угол между биссектрисой и высотой, проведенными из вершины прямого угла, равен половине разности острых углов этого треугольника.
Определяем неизвестный угол В для вариантов:
1) 90 -8 = 82 градусів
2) 90 - 32 = 58 градусів
3) 90 - 28 = 62 градусів
4) 90 - 18 = 72градусів.
Находим половину разности острых углов.
1) 82 - 8 = 74 градусів
2) 58 - 32 = 26 градусів
3) 62 - 28 = 34 градусів
4) 72 - 18 = 54 градусів.
Теперь находим угол КСН:
1) 74 / 2 = 37 градусів ответ В).
2) 26 / 2 = 13 градусів ответ Г).
3) 34 / 2 = 17 градусів ответ Д).
4) 54 / 2 = 27 градусів. ответ А).
12 см.
Объяснение:
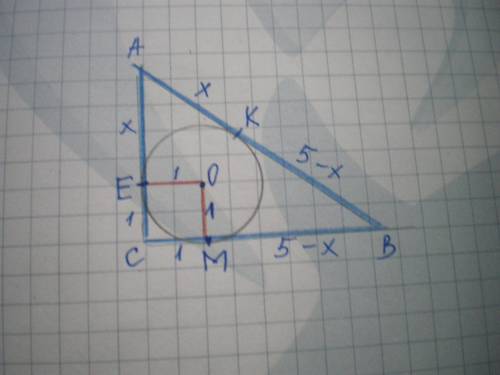
Дано: ΔАВС - прямокутний, ∠С=90°, АВ=5 см, ОЕ-радіус, ОЕ=1 см. Знайти Р(АВС).
Нехай коло торкається гіпотенузи у точці К, катета АС у точці Е, катета ВС у точці М.
Відрізки дотичних, проведених з однієї точки до кола, рівні між собою.
Нехай АК=х см, тоді ВК-5-х см; але АЕ=АК, отже, АЕ=х см.
ВМ=ВК=5-х см.
Дотична до кола перпендикулярна до радіуса, проведеного у точку дотику. Тому СЕ⊥ЕО, ОМ⊥СМ, ЕС⊥СМ, ЕО=ОМ як радіуси, отже ОЕСМ - квадрат, ЕС=СМ=1 см.
АС=х+1 см.
Знайдемо периметр АВС:
Р=АВ+АС+ВС=5+(х+1)+(1+5-х)=5+х+1+1+5-х=12 см.
1 .а
2.б.
3.а.
4.а.
5.б
6.а..
7.