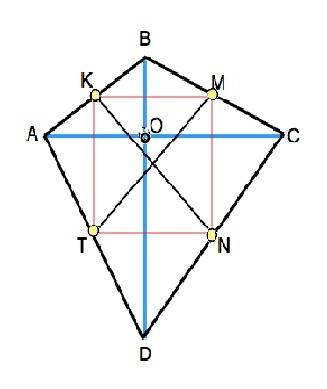
Пусть дан четырёхугольник АВСD. Точка К - середина АВ, т.М - середина ВС, N и Т - середины СD и DA соответсвенно. По условию КN=ТМ. Проведем диагонали АС и ВD. Соединим середины сторон треугольников АВС, ВСD, CDA и DAB. В треугольниках АВС и АDC средние линии параллельны и равны половине диагонали АС исходного четырехугольника.⇒ КМ параллельна и равна ТN. Аналогично доказывается КТ=МN. Противоположные стороны КМNТ параллельны и равны. КМNТ - параллелограмм с равными диагоналями ( КN=МТ по условию), т.е. КМNТ - прямоугольник. А раз стороны КМNТ пересекаются под прямым углом, то и диагонали четырехугольника АВСD, которым они параллельны, также пересекаются под прямым углом, ч.т.д.
Диагонали ромба пересекаются под прямым углом. Если на диагоналях ромба от точки их пересечения отложены четыре равных отрезка, то в полученном четырехугольника получится, что диагонали равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы четырехугольника пополам (то, что делят углы пополам видно из того, что диагоналями четырёхугольник делится на 4 равных равнобедренных прямоугольных треугольника, у которых катеты -это половина диагоналей, а гипотенуза - сторона четырехугольника; следовательно углы при гипотенузе равны по 45 градусов). Углы полученного четырехугольника - прямые. Все это относится к свойствам квадрата, значит четырёхугольник -квадрат, что и требовалось доказать.
∠PPC=100°
Объяснение:
Точка Р лежит внутри равнобедренного △ABC (AB=BC). ∠ABC=80°, ∠PAC=40°, ∠ACP=30°. Требуется найти ∠BPC.
Так как в равнобедренном треугольнике углы при основании равны, то
∠BAC=∠BCA=(180°-∠ABC)÷2=(180°-80°)÷2= 50°
∠BCP =∠BCA-∠ACP=50°-30°= 20°,
∠BAP =∠BAC-∠PAC=50°-40°= 10°.
Построим на стороне ABC равносторонний треугольник ABD.
В равностороннем треугольнике все углы равны 60°: ∠DAB=∠ABD=∠ADB=60°.
Проведём диагональ CD в четырёхугольнике ABCD. Так как AB=BC по условию, а BD=AB по построению, то BD= BC. Следовательно △CBD - равнобедренный. ∠BDC=∠BCD=(180°-∠DBC)÷2=(180°-(∠ABD+∠ABC))÷2=(180°-(60°+80°))÷2=20°.
Так как ∠BCP также равен 20°, то точка P лежит на стороне CD.
△ADP.
∠DAP=∠DAB+∠BAP=60°+10°= 70°.
∠ADP=∠ADB-∠BDC=60°-20°= 40°.
Следовательно ∠DPA=180°-∠DAP-∠ADP=180°-70°-40°= 70°.
Таким образом ∠DAP=∠DPA, следовательно △ADP - равнобедренный.
DA=DP - как боковые стороны равнобедренного △ADP. Но:
DA=DB - как стороны равностороннего △ABD. Значит:
DP=DB. => △DBP - равнобедренный, ∠DBP=∠DPB=(180°-∠BDC)÷2=(180°-20°)÷2=80° - как углы при основании равнобедренного треугольника.
∠DPB и ∠BPC - смежные углы. Их сумма равна 180°:
∠BPC=180°-∠DPB=180°-80°= 100°.