1.пусть меньший катет равен х, тогда второй катет равен х+3. По условию составим уравнение:
х(х+3)/2=65 реши это квадратное уравнение. ответом будет значение х.
2. проложим к основанию высоту. она равна корню из разости 2 произведений 35*35-21*21
оно равно 28.
затем по формуле площади треугольника
S=28*42/2=588
3. проведём высоту из угла, прилежащего основанию. он равен (т.к. лежит против угла в 30 гр) половине гипотенузы или боковой стороны. уравнение
х*2х/2=529
х=23
2х=46 боковая сторона
Объяснение:
Рисунок к задаче в приложении.
Построить три заданных точки не очень трудно.
А вот четвёртую точку - С - построим силой Разума.
мысль 1 - стороны параллелограмма параллельны
мысль 2 - противоположные стороны равны - AD = BC.
мысль 3 - как точка D сдвинута от точки А, так и точка С сдвинута от точки В.
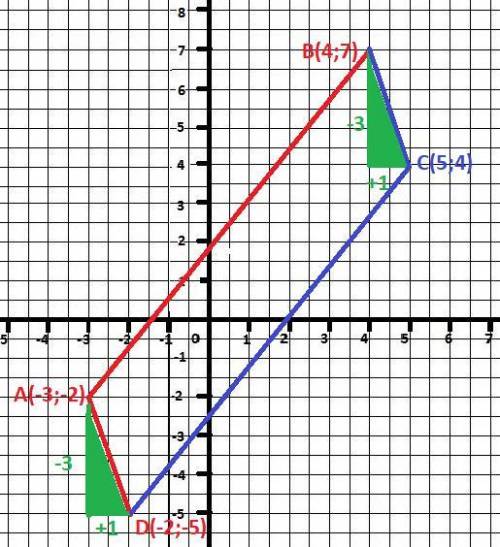
РЕШЕНИЕ
Вычисляем разность координат точек А и D.
dX = Dx - Ax = -2 - (-3) = +1 - сдвинута на 1 вправо.
dY = Dy - Ay = -5 - (-2) = - 3 - сдвинута на 3 вниз.
Такие же сдвигу применим к точке В и получим координату точки С.
Cx= Bx + 1 = 4 + 1 = 5
Cy = By - 3 = 7 - 3 = 4
ОТВЕТ: С(5;4) - координата точки С.
∠BMC=135°
Объяснение:
Первое решение.
В квадрате BACD построим внутрь равносторонний треугольник CMD. Получим два равнобедренных треугольника с углами 75. Тогда AMB с углами 15. Пришли к условию задачи, точка M единственная. ∠BMC=75+60=135°
Второе решение.
Построим △ANC, равный △AMB.
AM=AN, ∠MAN=90-15-15=60
△MAN -равносторонний (р/б с углом 60)
∠ANC=∠AMB=150
∠MNC=360-60-150=150
△MNC=△ANC (по двум сторонам и углу между ними)
∠NMC=∠NAC=15
∠BMC=360-150-60-15 =135°