Question

В равнобедренном треугольнике основание равно 10 см, высота, опущенная на боковую сторону равна 6 см. Найдите длину боковой стороны треугольника.

Answer 1

Боковая сторона треугольника равна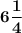 $\displaystyle\bf 6\frac{1}{4}$  см.

Объяснение:

В равнобедренном треугольнике основание равно 10 см, высота, опущенная на боковую сторону равна 6 см. Найдите длину боковой стороны треугольника.

Дано: ΔАВС = равнобедренный.

АС = 10 см - основание;

АН = 6 см - высота.

Найти: АВ.

1. Рассмотрим ΔАНС - прямоугольный.

По теореме Пифагора найдем НС:

Квадрат гипотенузы равен сумме квадратов катетов.

НС² = АС² - АН² = 100 - 36 = 64

НС = √64 = 8 (см)

2. Рассмотрим ΔАВН - прямоугольный.

Пусть АВ = ВС = а см, тогда ВН = (а - 8) см.

По теореме Пифагора:

АН² + НВ² = АВ²

6² + (а - 8)² = а²

36 + а² - 16а + 64 = а²

16а = 100     |:16

$\displaystyle\bf a=\frac{100}{16} a=6\frac{1}{4}$

$\displaystyle\bf AB = BC = a=6\frac{1}{4}\;_{(CM)}$

Боковая сторона треугольника равна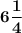 $\displaystyle\bf 6\frac{1}{4}$  см.