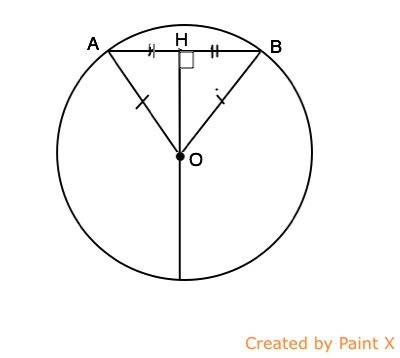
Соединим центр О окружности с концами хорды АВ. ОА=ОВ=R.
Треугольник АОВ - равнобедренный. Проведем высоту ОН этого треугольника.
Угол ОНВ=углу ОНА=90º
«Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один»
Следовательно, и к середине хорды можно провести только один перпендикуляр.
Высота ОН - медиана равнобедренного треугольника.
АН=ВН. Точка Н - середина АВ.
Следовательно, ОН, проходящий через середину АВ, есть срединный перпендикуляр хорды АВ, ч.т.д.
Відповідь:
Пояснення:
Я думаю , що в умові дано рівнобедрену трапецію . Тоді
BD - діагональ і бісектриса ∠В трапеції ABCD .
1) AD║BC , BD - січна , тоді ∠ADB = ∠CBD як внутрішні
різносторонні кути . Тому ΔABD - рівнобедрений : AD = AB = 17 см.
Проведемо ВМ⊥AD . У прямок. ΔАМВ АМ = ( AD - BC ) : 2 =
= ( 17 - 1 ) : 2 = 8 ( см ) . За Т. Піфагора ВМ = h = √( AB² - AM² ) =
= √( 17² - 8² ) = 15 ( см ) ; h = 15 см .
2) S трап = ( AD + BC ) * BM/2 = ( 17 + 1 ) * 15/2 = 135 ( см² ) ;
S трап = 135 см² .