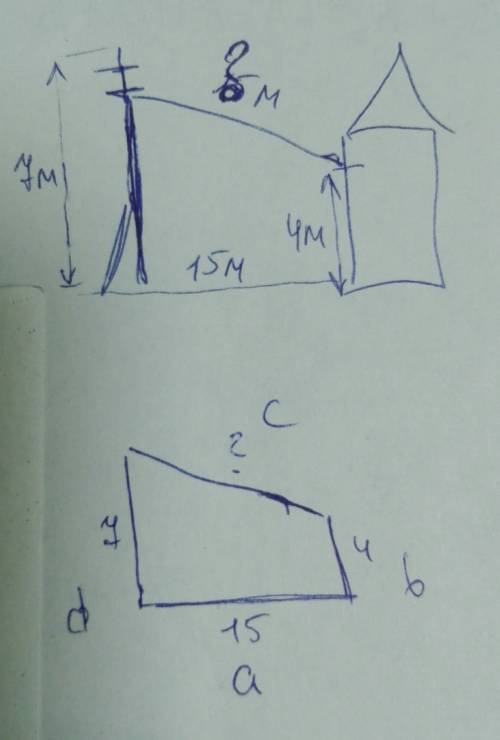
Опишем это, как перпендикулярную трапецию.
Прямоугольная трапеция является трапецией, у которой одна из боковых сторон перпендикулярна основаниям. Средняя линия прямоугольной трапеции равна половине суммы ее оснований m=(b+d)/2
Высота прямоугольной трапеции равна ее боковой стороне-перпендикуляру.
Вторая боковая сторона прямоугольной трапеции, находящаяся под углом к основаниям, отличным от 90 градусов, вычисляется по теореме Пифагора в прямоугольном треугольнике с высотой. c=√(h^2+〖(d-b)〗^2 )=√(a^2+〖(d-b)〗^2 )
с=√(a^2+〖(d-b)〗^2 )=15,297м
Плюс 15%
Кабель = 15,297+2,293= 17,59м
Доказательство. Рассмотрим треугольники ABC и A1B1C1, у которых AB = A1B1, BC = B1C1, CA = C1A1 (рис. 84), и докажем, что эти треугольники равны.
Равные треугольники по трем сторонам
Приложим треугольник ABC к треугольнику A1B1C1 так, чтобы вершина A и A1, B и B1 совместились, а вершины C и C1 оказались по разные стороны от прямой A1B1 (рис. 85, а). Проведем отрезок CC1. Если он пересекает отрезок A1B1, то получим два равнобедренных треугольника: A1C1C и B1C1C (рис. 85, б). Значит, ∠1 = ∠2 и ∠3 = ∠4, и, следовательно, ∠C = ∠C1. Итак, AC = A1C1, BC = B1C1 и ∠С = ∠С1, поэтому треугольники ABC и A1B1C1 равны по первому признаку равенства треугольников.
Доказательство равенства треугольников по трем сторонам
Кроме рассмотренного нами случая (рис. 85, б), возможны еще два (рис. 86, а, б). Доказательства равенства треугольников ABC и A1B1C1 в этих случаях приведены на рисунках 86, а, б. Теорема доказана.
41) △ABC - равносторонний, все углы по 60°.
Рассмотрим △FCE
∠FEC=90°, ∠С=60°, ∠F=90°-∠C=30°
Катет против угла 30 равен половине гипотенузы.
CE=FC/2=(8+12)/2=10
AE=AC-CE=12-10=2
42) Площади треугольников с равным углом относятся как произведения прилежащих сторон.
Пусть AD=...=x, BS=...=y
S(EBN)/S(ABC) =BE*BN/BA*BC =3x*3y/5x*4y =9/20
Треугольники SNE и EBN имеют общую высоту из вершины E.
Площади треугольников с равными высотами относятся как основания.
S(SNE)/S(EBN) =SN/BN =2y/3y =2/3
S(SNE)/S(ABC) =2/3 *9/20 =3/10
43) Продлим CB и DA до пересечения в точке E.
△ABC - равносторонний, все углы по 60° (∠E=180°-∠C-∠D=60°)
△EBA - прямоугольный с углом 30° (∠EBA=90°-∠E=30°)
Катет против угла 30° равен половине гипотенузы.
Пусть EA=y, тогда EB=2y
EC=ED=CD => 2y+6 =y+8 => y=2
CD=8+2=10