1)
Центральный угол в развёртке боковой поверхности конуса равен 120°. Высота конуса=4√2. Найдите его объем.
----------
Образующая конуса L- радиус окружности с центром В, частью которой является его развертка АВС.
Формула длины окружности =2πR =2πL, где L- образующая конуса.
Т.к. угол АВС=120°, а полная окружность содержит 360°, длина дуги АС=1/3 длины окружности, содержащей развертку конуса.
◡AC=2πL/3
В то же время дуга АС этой окружности равна длине окружности основания конуса.
2πr=2πL/3 ⇒ L=3r
Из треугольника, образованного высотой конуса и радиуса ( катеты) и образующей ( гипотенуза) найдем по т.Пифагора радиус основания конуса.
L²-r²=h²
9r²-r²=32
r²=32:8=4
V(кон)=πr²•h/3
V=(π4•4√2):3=(π16√2):3
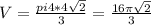 (ед. объёма)
(ед. объёма)
2)
В правильной треугольной пирамиде расстояние от вершины основания до противолежащей боковой грани= m. Боковые грани наклонены к основанию под углом a (альфа). Найдите объем вписанного в пирамиду конуса.
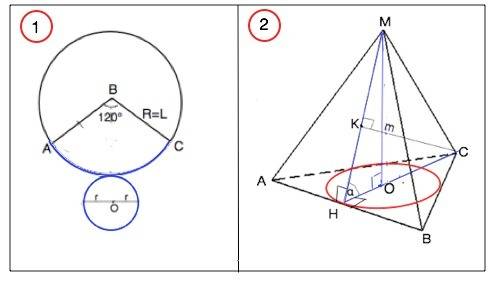
Правильная пирамида МАВС – это пирамида, основанием которой является правильный треугольник АВС, а вершина М пирамиды проецируется в центр О этого треугольника.
Образующей вписанного в пирамиду конуса является апофема пирамиды, а основание этого конуса ограничено окружностью, вписанной в основание пирамиды, т.е. в ∆ АВС.
Радиус конуса равен 1/3 высоты СН правильного треугольника АВС
Расстояние от вершины С основания АВС до грани АМВ - высота треугольника СМН, плоскость которого перпендикулярна грани АМВ и основанию АВС.
Угол α образован прямыми СН и МН, перпендикулярными ребру АВ в точке Н.
r=OН=(КС:sinα):3=(m:sinα):3 =m:3sinα ⇒
высота МО=OH•tgα=(m:3sinα):sinα/cosα=m:3cosα
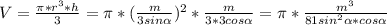
Сейчас я попробую, что-нибудь решить.
Я же всё-таки не знаток, мне недавно 16 исполнилось.
S1(Площадь правильного треугольника)=корень из 3 делим на 4 и умножаем на сторону в квадрате=SQRT3/4*a*a
S2(площадь тетраэдра)=S1*4(так как в тетраэдре 4 равносторонних треугольника)=SQRT(3)*a*a=30*SQRT3
То есть a*a=30
а=SQRT(30)
h(высота)=SQRT6/3*a=4,4721...=4,47
Теперь найду основание конуса.
Радиус вписанной окружности равен.
r=a*SQRT3/6=1,5811=1,58
S3(Вся площадь конуса)=ПЛощади окружности + площади боковой стороны=r*r*П=7,85374999 + П*r*SQRT(r*r+h*h) =7,85 +23,55 =31,4 дм в квадрате
Я очень надеюсь, что правильно, заметь, конусы и тетраэдры я не проходил нигде, просто соображаю неплохо!!
Скажи
***
МО - высота, которая равна √3
MA - ребро правильного тетраэдра
АО = MA√3/3
(как радиус окружности, описанной около правильного треугольника)
из прям. треугольника AОМ по теореме Пифагора:
(в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов)
c² = a² + b²
MA² = MO² + (MA√3/3)²
MA² = MO² + MA²/3
2MA²/3 = MO²
MA² = 3MO²/2
MA² = (3 · 3)/2 = 9/2 = 4.5 ед.
площадь боковой поверхности тетраэдра будет равна трем площадям треугольников,
и поскольку площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
SΔ = ah = AO · MO
S = MA√3/3 · √3 = 1 · 4,5 = 4.5 кв. ед.
⇔
S (б.п) = 3 · 1/2ah = 3 · 4,5 = 13,5 кв. ед.
ответ: площадь боковой поверхности правильного тетраэдра равна
13,5 кв. ед.