Question

Диагональ равносторонней трапеции перпендикулярна боковой стороне, а угол между боковой стороной и большим основанием трапеции равен . Найдите радиус окружности, описанной вокруг
трапеции, если ее высота равна h.

Answer 1

$\displaystyle\frac{h}{{2\sin \alpha \cos \alpha }}=\displaystyle\frac{h}{{\sin 2\alpha }}$

Объяснение:

Используя метрические соотношения в прямоугольном треугольнике из треугольника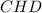 $CHD$ получаем:

$\sin \alpha = \displaystyle\frac{{CH}}{{CD}};$

$CD = \displaystyle\frac{h}{{\sin \alpha }}.$

Тогда из треугольника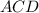 $ACD$

$\cos \alpha = \displaystyle\frac{{CD}}{{AD}};$

$AD = \displaystyle\frac{{CD}}{{\cos \alpha }} = \displaystyle\frac{h}{{\sin \alpha }}:\cos \alpha = \displaystyle\frac{h}{{\sin \alpha }} \cdot \displaystyle\frac{1}{{\cos \alpha }} = \displaystyle\frac{h}{{\sin \alpha \cos \alpha }}.$

Описанная окружность трапеции одновременно является описанной окружностью вокруг прямоугольного треугольника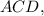 $ACD,$ значит ее радиус равен половине гипотенузы:

$R = \displaystyle\frac{{AD}}{2} = \displaystyle\frac{h}{{2\sin \alpha \cos \alpha }}.$

Пользуясь знаниями по тригонометрии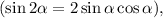 $(\sin 2\alpha = 2\sin \alpha \cos \alpha ),$ можно записать ответ компактнее:

$R = \displaystyle\frac{h}{{\sin 2\alpha }}.$