Объяснение:
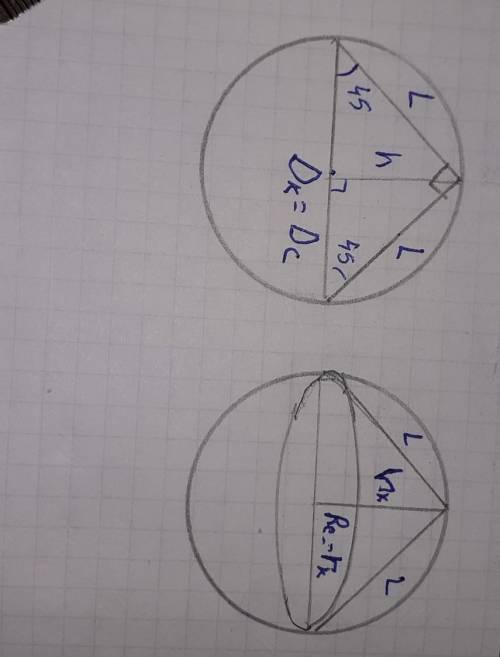
радиус сферы описанного около конуса равен радиусу конуса. так как центр основания конуса и центр сферы совпадают Rc=rк
радиус сферы описанного около конуса равен высоте конуса Rс=rк=Hк.
высота конуса перпендикулярно к основанию конуса.
при осевом сечении конуса выходит фигура равнобедренный прямоугольный треугольник.
где образующая L конуса катеты, а основание гипотенуза равное диаметру Dк конуса. По теореме Пифагора. а²+в²=с²
находим гипотенузу равную диаметру D=2R
Dк=√L²+L²
Dк=√(7√2)²+(7√2)²=√49×2+49×2=√98+98=√196=14
Dк=Dс=14
радиус сферы
Rc=Dc/2=14/2=7
Объяснение:
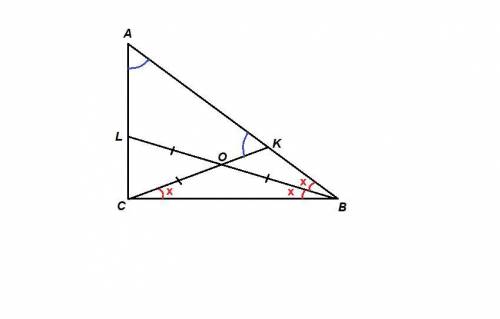
ΔLBC: ∠LCB = 90°, О - середина гипотенузы LВ, ⇒ СО - медиана, проведенная к гипотенузе, равна половине гипотенузы. Значит
ВО = OL = ОС.
Пусть половине угла В - х.
∠ОСВ = ∠ОВС = х, как углы при основании равнобедренного треугольника ОВС.
Тогда ∠АСК = 90° - х.
ΔАСК равнобедренный, так как СК = АС по условию, значит
∠САК = ∠СКА = (180° - ∠АСК) / 2 =
= (180° - (90° - x)) / 2 = (180° - 90° + x) / 2 = (90° + x) / 2
Сумма острых углов прямоугольного треугольника равна 90°:
∠САК + ∠АВС = 90°
Получаем уравнение:
(90° + x) / 2 + 2x = 90° | ·2
90° + x + 4x = 180°
5x = 90°
x = 18°
∠ABC = 2 · 18° = 36°
см фото
Объяснение: