угол Е=57; угол F=17
Объяснение:
угол F=17, а L=106
17+106=123
180-123=57
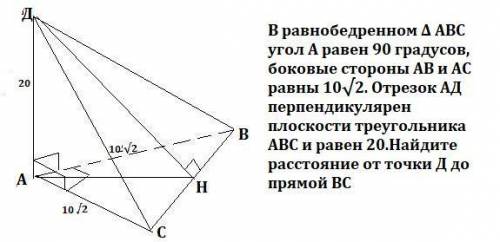
В равнобедренном Δ ABC угол А равен 90 градусов, боковые стороны AB и АC равны 10√2. Отрезок АД перпендикулярен плоскости треугольника АВС и равен 20.Найдите расстояние от точки Д до прямой ВС
Объяснение:
Пусть ДН⊥ВС. Тогда расстоянием от точки Д до прямой ВС будет отрезок ДН .
По т. о трех перпендикулярах АН⊥ВС.
1)ΔАВС-прямоугольный, по т Пифагора ВС=√((10√2)²+(10√2)² )=20.
2)В ΔАBС равнобедренном , высота АН является медианой ⇒
ВН=10 см.
3) ΔАВН -прямоугольный , по т. Пифагора ДH=√( (10√2)²-10²)= 10 (см).
6 см²
Объяснение:
Пусть ABCD – трапеция, CD = 2 см, АВ = 3 см, BD = 3 см и АС = 4 см. Чтобы известные элементы включить в один треугольник, перенесём диагональ BD на вектор DC в положение СВ'. Рассмотрим треугольник АСВ1. Так как ВВ'CD – параллелограмм, то В'С = 3 см, АВ' = АВ + ВВ' = АВ + CD = 5 см. Теперь известны все три стороны треугольника АВ'С. Так как АС²+ В'С²= АВ'²= 16+9=25, то треугольник АВ'С – прямоугольный, причем АСВ' = 90°. Отсюда непосредственно следует, что угол между диагоналями трапеции, равный углу АСВ', составляет 90°. Площадь трапеции, как и всякого четырёхугольника, равна половине произведения диагоналей на синус угла между ними. Отсюда площадь равна 1/2AC * BD * sin 90° = 1/2 * 4 * 3 * 1 = 6 см²
Объяснение:
∠LFE=17 ° - как вертикальные.
сумма углов треугольника равна 180°:
∠FEL=180-∠LFE-∠FLE=180-17-106=57°
ответ: 17° ; 57°