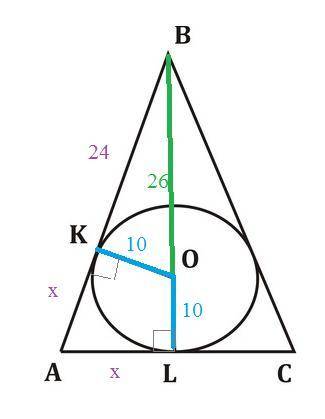
Стороны треугольника являются касательными к окружности.
Касательная перпендикулярна радиусу, проведенному в точку касания.
ОК⊥АВ
OL⊥AC
Высота равнобедренного треугольника, проведённая к основанию, одновременно и медиана и биссектриса.
AL=LC
ОК=ОL=10 см
BO=26 см
По теореме Пифагора
BK²=BO²-OK²=26²-10²=676-100=576
BK=24 см
Пусть AK=x
По свойству касательных, проведенных к окружности из одной точки
AK=AL=x
По теореме Пифагора из прямоугольного треугольника АВL:
AB²-AL²=BL²
(24+x)²-x²=(10+26)²
24²+48x+x²-x²=36²
48x=720
x=15
AC=2AL=30 см
S(Δ ABC)=(1/2)AC·BL=(1/2)·30·36=540 кв см.
відповідь:
Основания трапеции параллельны, значит ∠FBC = ∠FAD как соответственные при пересечении параллельных прямых ВС и AD секущей AF, угол при вершине F общий для треугольников BFC и AFD, ⇒
ΔBFC подобен ΔAFD по двум углам.
АВ составляет 3 равных части, а BF 7 таких же частей, тогда AF составляет 10 равных частей.
BC : AD = BF : AF
x / (x + 6) = 7 : 10
10x = 7(x + 6)
10x = 7x + 42
3x = 42
x = 14 см
AD = 14 + 6 = 20 см
Пояснення:Надеюсь правильно!