Дано:
∆АВС
∆2,3 = ?
АВС•2=2АВС
Значит:
А=19°
В=12°
С=12°
Объяснение:
думаю так
Эту задачу можнорешить двумя .
1) Более лёгкий - геометрический.
Используется свойство: расстояние между прямыми L1 и L2 равно расстоянию от любой точки прямой L1 до плоскости P, параллельной прямой L1 и в которой находится прямая L2.
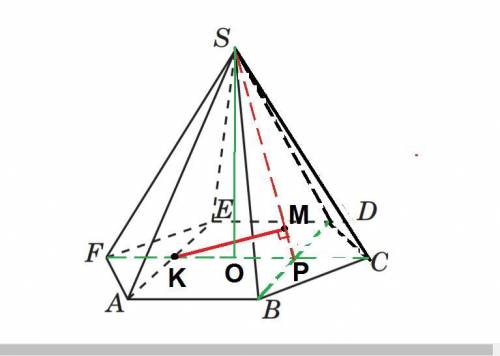
Проведём плоскость SBD, параллельную отрезку АЕ. След её сечения основания- это прямая BD.
Проведём секущую перпендикулярную плоскость FSC.
Точки К и Р это середины проекций боковых рёбер на основание.
В сечении имеем 2 равнобедренных треугольника FSC и KSP.
Высота их равна высоте пирамиды и равна √3 как высота равностороннего треугольника FSC со стороной 2.
Длина перпендикуляра КМ и есть искомое расстояние L1_L2.
Площадь KSP = (1/2)*1*√3 = √3/2.
Тогда КМ = 2S/(PS). Находим PS = √((√3)² + (1/2)²) = √13/2.
ответ: КМ = 2*(√3/2)/(√13/2) = 2√3/√13 = 2√39/13.
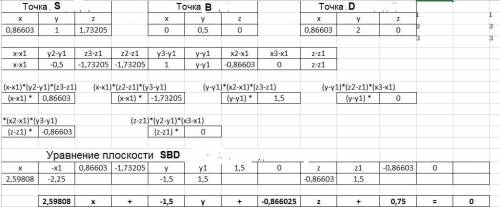
2) Векторный или координатный.
Пусть вершина А на оси Ох в точке х = (√3/2), сторона ВС по оси Оу.
Наименование вершин по часовой стрелке.
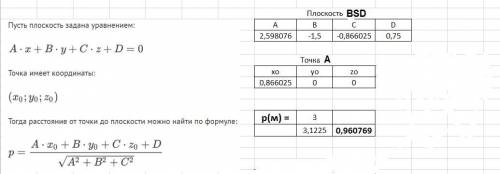
Решение дано во вложениях как копии расчёта в программе Excel.
ответ дан числом в десятичной системе, но его значение соответсвует найденному в варианте 1).
1. Нарисуем рисунок.
2. Рассмотрим треугольник DBE.
Это равнобедренный треугольник, так как по условию BD = BE.
∠BDE = ∠BED, так как это углы при основании равнобедренного треугольника.
3. Определим ∠BDA и ∠BEC.
∠BDA и ∠BDE смежные, поэтому
∠BDA = 180° - ∠BDE.
Аналогично ∠BEC и ∠BED смежные, поэтому
∠BEC = 180° - ∠BED.
Так как ∠BDE = ∠BED, то и ∠BDA = ∠BEC.
4. Рассмотрим треугольники ABD и CBE.
Эти треугольники равны по двум сторонам и углу между ними:
BD = BE и AD = CE - по условию;
∠BDA = ∠BEC.
Следовательно, и стороны BA и BC равны.
Значит, треугольник ABC -равнобедренный.
Для того, чтобы найти углы треугольника, нам нужно знать хотя бы один угол или одну сторону треугольника. Если даны все стороны и углы треугольника, то мы можем воспользоваться формулами тригонометрии для нахождения оставшихся углов.
Если известны только стороны треугольника, то мы можем воспользоваться теоремой косинусов или теоремой синусов.
Теорема косинусов гласит:
c^2 = a^2 + b^2 - 2ab*cos(C)
где c - длина стороны, противолежащей углу C, a и b - длины двух других сторон, а cos(C) - косинус угла C.
Используя теорему косинусов, мы можем найти косинус каждого угла и затем найти сам угол, используя обратную функцию косинуса (arccos). Таким образом, мы можем найти все углы треугольника.
Если даны углы треугольника, то мы можем воспользоваться свойством, согласно которому сумма углов треугольника равна 180 градусам. Таким образом, мы можем найти третий угол, вычитая из 180 градусов сумму двух данных углов.
Без дополнительной информации о треугольнике нельзя точно определить его углы. Если есть дополнительные данные , уточните вопрос.
Объяснение: