Построение сводится к проведению перпендикуляра из точки к прямой.
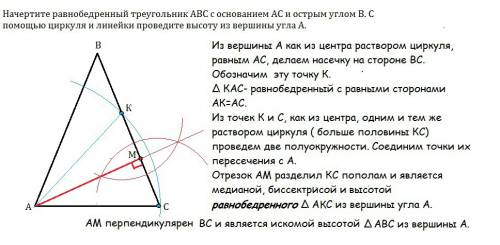
Из вершины А, как из центра, раствором циркуля, равным АС, делаем насечку на стороне ВС. Обозначим эту точку К.
∆ КАС- равнобедренный с равными сторонами АК=АС.
Разделив КС пополам, получим точку М, в которой медиана ∆ КАС пересекается с основанием КС. Т.к. в равнобедренном треугольнике медиана=биссектриса=высота, отрезок АМ будет искомой высотой.
Для этого из точек К и С, как из центра, одним и тем же раствором циркуля ( больше половины КС) проведем две полуокружности. Соединим точки их пересечения с А.
Отрезок АМ разделил КС пополам и является искомой высотой ∆ АВС из вершины угла А.
Координаты точки А относительно оси абсцисс ( 3; 4)
Координаты точки В относительно оси ординат ( 0; - 5)
Координаты точки А относительно начала координат (3; -4)
Координаты точки В относительно начала координат ( -0; -5)
Объяснение:
На координатной плоскости координаты точек, симметричных относительно точки О начала координат, являются противоположными числами.
Например:
Дано:точка А (8;-3)
Найти:Точка В симметричная точке А относительно начала координат
По объяснению выше мы можем без труда узнать,что координаты точки В являются противоположными координатам точки А, значит (-8;3)
Рада была