За кутами
Гострокутний - всі кути гострі (якщо a, b, c - сторони трикутника, причому с - найбільша, то c2<a2+b2
Прямокутний - один з кутів прямий (якщо a, b, c - сторони трикутника, причому с - найбільша, то c2=a2+b2
Тупокутний- один з кутів тупий (якщо a, b, c - сторони трикутника, причому с - найбільша, то c2>a2+b2
За сторонами
Різносторонній - всі сторони різні
Рівнобічний- дві сторони рівні (називаються бічними, третя - основою)
Рівносторонній (правильний) - всі сторони рівні
Медіана - відрізок, який сполучає вершину трикутника з серединою протилежної сторони (ділить сторону навпіл). Медіани трикутника перетинаються в одній точці і точкою перетину діляться у відношенні 2:1, починаючи від вершини)
Висота - відрізок, який проведений з вершини трикутника перпендмикулярно до протилежної сторони
Бісектриса, відрізок, який проведено з вершини до протилежної сторони і який ділить кут навпіл. Бісектриси трикутника перетинаються в одній точці і ділять протилежну сторону на відрізки, пропорційні прилеглим сторонам трикутника (якщо АК - бісектриса трикутника АВС, то ВК:КС=АВ:АС)
Середня лінія трикутника - відрізок, який сполучає середини двох сторін трикутника. Середня лінія трикутника паралельна третій стороні трикутника і дорівнює її половині
Гіпотенуза - найбільша сторона прямокутного трикутника (лежить напроти прямого кута), катети - дві інші сторони прямокутного трикутника
Центр кола, описаного навколо трикутника, знаходиться в точці перетину серединних перпендикулярів. В прямокутному трикутнику він знаходиться на середині гіпотенузи
Центр кола, вписаного в трикутник, знаходиться в точці перетину бісектрис трикутника
Объяснение:
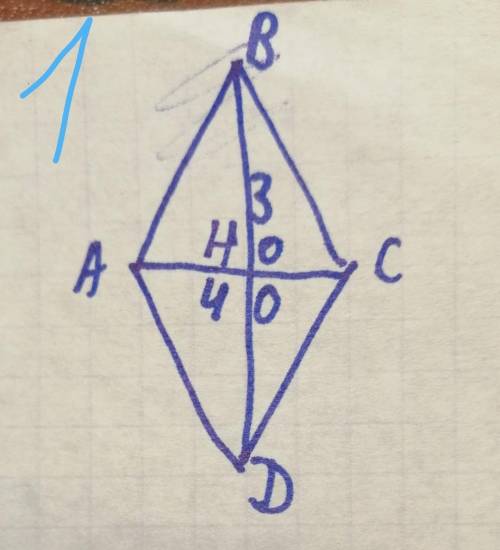
1). АС перпендикулярен ВD т.к. АВСD - ромб (Н - точка пересечения диагоналей)
ВН = НD = 30÷2 = 15
АН = НС = 40÷2 = 20
треуг. АНВ - прямоуг.
По т. Пифагора
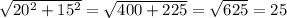
P = 25 * 4 = 100
ответ: 100
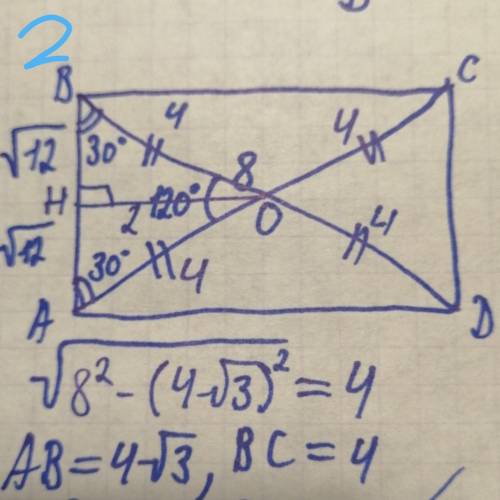
2). Проведем ОН перпендикулярно АВ
АО = ОС = ОВ = ОD (диагонали прямоугольника точкой пересечения делятся пополам)
угол ВОН = углу НОА = 60°
треуг. ВНО - прямоуг., угол НВО = 30° => ОН = 1/2 ОВ = 2
По т. Пифагора
НВ=
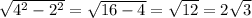
АВ = 2НВ = 4 корня из 3
треуг. АВD - прямоуг
По т. Пифагора
АD =
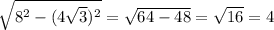
ответ: 2 стороны по 4 корня из 3, 2 стороны по 4
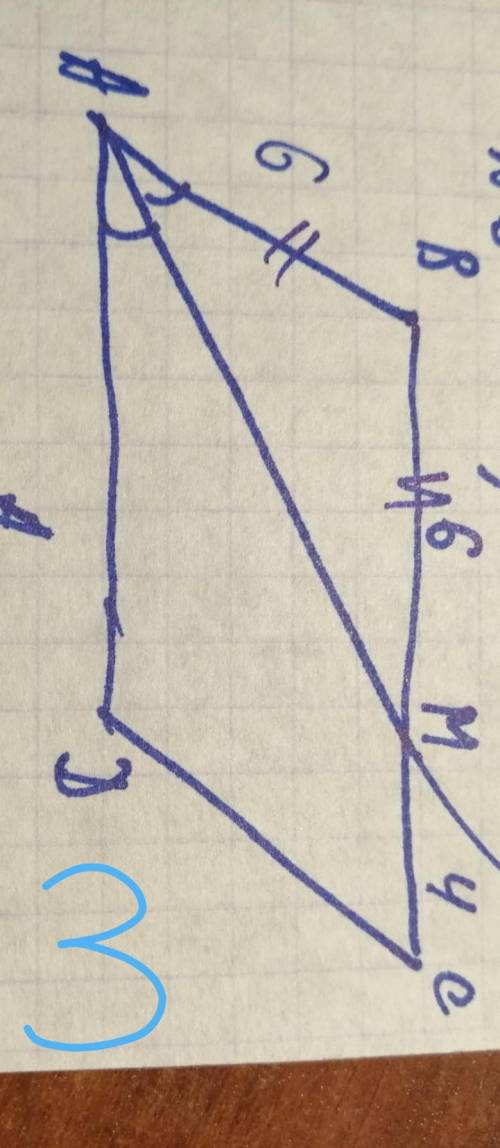
3). Биссектриса параллелограмма отсекает от него р/б треуг. => ВМ = АВ = 6
ВС = ВМ + МС = 6 + 4 = 10
Р = 6 + 6 + 10 + 10 = 32
ответ: 32
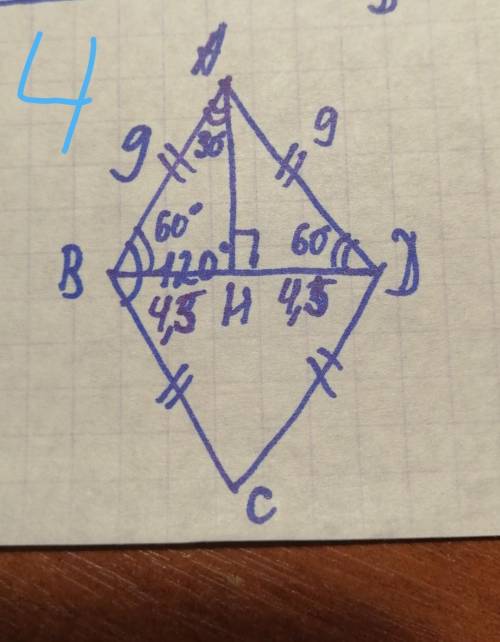
4). АВ = АD = 36÷4 = 9
Проведем АН перпендикулярно ВD
треуг. АВD - р/б, угол АВD = 120°÷2 = 60°
треуг. АВН - прямоуг., угол ВАН = 90° - 60° = 30° => ВН = 1/2 АВ = 4,5 (катет, лежащий против угла в 30°, равны половине гипотенузы)
ВD = 2ВН = 9
ответ: 9
5). Проведем ОН перпендикулярно СD
угол СОН = углу HOD = 60°÷2 = 30°
треуг. СОН - прямоуг., угол СОН = 30° => СН = 1/2 ОС = 1,5 (катет, лежащий против угла в 30°, равны половине гипотенузы) => CD = 3
треуг. АСD - прямоуг.
По т. Пифагора
АD=
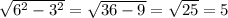
S = 3 * 5 = 15
ответ: 15