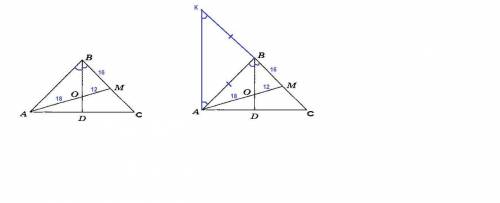
ВD - высота равнобедренного треугольника, проведенная к основанию, значит и биссектриса.
Биссектриса треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам.
В треугольнике АВМ ВО - биссектриса, значит
АО : ОМ = ВА : ВМ
ВА = АО · ВМ / ОМ = 18 · 16 / 12 = 24 см
Доказательство свойства биссектрисы (на всякий случай)
Проведем прямую АК║BD, К - точка пересечения этой прямой с прямой ВС.
∠DBA = ∠KAB как накрест лежащие (AK ║ BD, AB секущая),
∠CBD = ∠СКА как соответственные (АК ║ BD, СК секущая),
так как ∠DBA = ∠CBD, то и ∠КАВ = ∠СКА, тогда
ΔАВК равнобедренный, АВ = ВК.
По обобщенной теореме Фалеса:
АО : ОМ = КВ : ВМ или
АО : ОМ = АВ : ВМ.
Щоб довести рівність трикутників ABC і BAD, ми маємо показати, що вони мають рівні сторони та рівні кути.
Рівні сторони:
Так як точка О є серединою відрізків AB і CD, то ОА = ОВ та ОС = ОD.
Рівні кути:
За умовою, точка О є серединою відрізків AB і CD. Це означає, що відрізки OA і OB мають однаковий кут з відрізками OC і OD. Таким чином, ми маємо:
∠OAB = ∠OCD (користуємось фактом, що OA = OB та OC = OD, оскільки О є серединою відрізків AB і CD).
Аналогічно, ми можемо сказати:
∠OBA = ∠ODC.
Отже, трикутники ABC і BAD мають рівні сторони та рівні кути, що доводить їх рівність за принципом двох рівних сторін та рівного кута (SAS - side-angle-side).
P. S. Можно лучший ответ? (надо для нового статуса)