38 см
Объяснение:
1) Из верхнего основания опустим перпендикуляры на нижнее основание - получим 2 равны между собой прямоугольных треугольника (по краям) и прямоугольник - между ними.
2) Так как трапеция равнобедренная, то основания у двух полученных треугольников равны между собой и равны:
(17 - 13) : 2 = 4 : 2 = 2 см.
3) Рассмотрим треугольник. Его основание равно 2 см, а острый угол между боковой стороной и нижним основанием трапеции, согласно условию, равен 60 градусам.
Так как этот треугольник является по построению прямоугольным, то его сторона 2 см является катетом, который лежит против угла 30 градусов:
180 градусов (сумма внутренних углов треугольника) - 90 градусов (прямой угол) - 60 градусов (известный угол) = 30 градусов.
4) Катет 2 см, лежащий против угла 30 градусов, равен половине гипотенузы. А гипотенуза - это боковая сторона трапеции, которую нам надо найти, чтобы рассчитать периметр.
2 = х /2, где х - гипотенуза (она же - боковая сторона трапеции),
откуда х = 2 * 2 = 4 см (неизвестное делимое равно произведению делителя на частное).
5) Так как трапеция равнобедренная, то её боковые стороны равны между собой.
Находим периметр трапеции: 17 + 4 + 13 + 4 = 38 см
ответ: периметр данной трапеции равен 38 см.
1.
P(4;3), T(-2;5).
Используем уравнение прямой, проходящей через две точки.
Если даны две точки A(x₁; y₁) и B(x₂; y₂), тогда уравнение прямой, проходящей через эти две точки будет
То есть у нас даны две точки P(4;3) и T(-2;5), уравнение прямой, проходящей через них будет
-(x-4) = 3·(y-3),
4 - x = 3y - 9,
3y + x - 9 - 4 = 0,
x + 3y - 13 = 0.
Можно сделать проверку: подставим координаты каждой точки в уравнение и проверим выполнение равенства.
P(4;3):
4 + 3·3 - 13 = 4 + 9 - 13 = 0. Верно.
T(-2;5):
(-2) + 3·5 - 13 = -2 + 15 - 13 = 0. Верно.
ответ. x + 3y - 13 = 0.
2.
x + 3y - 13 = 0,
Уравнение оси Ox (оси абсцисс): y = 0. Подставим это в уравнение прямой и получим x + 3·0 - 13 = 0, ⇔ x = 13.
Итак, пересечение прямой с осью Ox дает точку (13;0).
Уравнение оси Oy (оси ординат): x = 0. Подставим это в уравнение прямой и получим 0 + 3y - 13 = 0, ⇔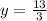 .
.
Итак, пересечение прямой с осью Oy в точке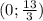 .
.
3.
Дана прямая x - y + 2 = 0 и окружность (x-2)² + (y-1)² = 9.
Чтобы найти координаты точек пересечения решим систему двух уравнений на два неизвестных.
Из уравнения прямой находим y = x+2, подставим это в уравнение окружности: (x-2)² + ( x+2 - 1)² = 9,
(x-2)² + (x+1)² = 9,
x² - 4x + 4 + x² + 2x + 1 = 9,
2x² - 2x + 5 - 9 = 0,
2x² - 2x - 4 = 0,
x² - x - 2 = 0,
D = (-1)² - 4·1·(-2) = 1 + 8 = 9 = 3²,
Итак, координаты первой точки (-1; 1).
Итак, координаты второй точки (2; 4).
ответ. (-1; 1), (2; 4).