Дано:
S=320
h=8
Основания относятся друг к другу как 3:5
Найти: основания
1. Сначала напишем формулу вычисления площади трапеции
S=a+b×h/2
2. Основания можно выразить через коэффициент пропорциональности-x, следовательно получается:
3х и 5х
3. Подставим все значения и решим уравнение:
320=3х+5х×8/2
320=8х×8/2
320=64х/2
64х=320×2
64х=640
х=640/64
х=10
4. Теперь подставим вместо х числа и получим значения оснований:
3х=3×10=30
5х=5×10=50
Если подставить значения оснований и найти площадь получится 320
30+50×8/2=80×8/2=640/2=320
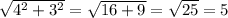 . Значит, сторона ромба равна 5 см (в ромбе все стороны равны).
. Значит, сторона ромба равна 5 см (в ромбе все стороны равны).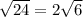 см.
см.
ответ: координаты D(1; 0), координаты середины отрезка О(3; 2).
Объяснение:
Нужно знать:
1) диагонали параллелограмма точкой пересечения делятся пополам;
2) координаты середины отрезка: х = (х₁ + х₂)/2, у = (у₁ + у₁)/2, где
(х₁; у₁) и (х₂; у₂) - концы отрезка.
Поэтому:
АС и ВD - диагонали, О - точка их пересечения, значит, ее координаты (как середины АС) равны: х = (1 + 5)/2 = 3, у = (2 + 2)/2 = 2, т.е. О(3; 2).
Эта же точка О - середина и диагонали ВD, тогда координаты точки D ббудут таковы: (5 + х)/2 = 3; (4 + у)/2 = 2, откуда х = 3 · 2 - 5 = 1, у = 2 · 2 - 4 = 0, т.е. D(1; 0).