ответ: V=a³•sin²α•tgβ/6
Объяснение - очень подробно:
Формула объема пирамиды V=S•h/3, где S – площадь основания пирамиды, h - её высота.
Стороны ромба равны. По условию боковые грани наклонены к плоскости основания под углом β.
Если боковые грани пирамиды наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проецируется в центр этой окружности.
Центр окружности, вписанной в ромб – точка пересечения его диагоналей, а расстояние от него до сторон равно радиусу вписанной окружности.
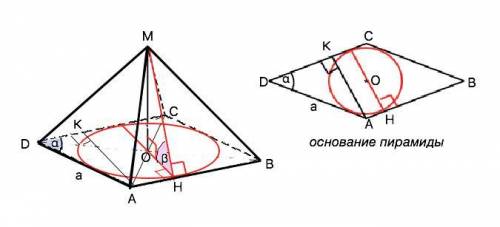
Высота пирамиды, радиус вписанной окружности и высота боковой грани образуют прямоугольный треугольник, при этом высота боковой грани и радиус вписанной окружности образуют линейный угол между основанием и боковой гранью, т.к. по т. о 3-х перпендикулярах перпендикулярны стороне ромба (ребру двугранного угла) в одной точке.
Диаметр окружности, вписанной в ромб, перпендикулярен его сторонам, параллелен высоте ромба и равен ей. На рисунке приложения АК = высота ромба. АК=АD•sinα=a•sinα ⇒ HO=r=a•sinα•1/2. Из прямоугольного ∆ МОН высота пирамиды МО=ОН•tgβ=(a•sinα•1/2)tgβ
S(ABCD)=AD•CD•sinα=a²•sinα
V=a²•sinα•(a•sinα•1/2)tgβ/3=a³•sin²α•tgβ/6
МА = 12 - расстояние от М до α,
МВ = 16 - расстояние от М до β.
Пусть плоскость АМВ пересекает ребро двугранного угла - прямую а - в точке С.
МА⊥α, а⊂α, значит МА⊥а.
МВ⊥β, а⊂β, значит МВ⊥а.
Так как прямая а перпендикулярна двум пересекающимся прямым плоскости АМВ, то она перпендикулярна этой плоскости, следовательно она перпендикулярна каждой прямой, лежащей в этой плоскости, ⇒
а⊥АС, а⊥ВС, ⇒∠АСВ = 90° - линейный угол двугранного угла;
а⊥МС, ⇒ МС - искомое расстояние.
МАСВ - прямоугольник, АС = МВ = 16.
Из прямоугольного треугольника АМС по теореме Пифагора:
МС = √(МА² + АС²) = √(16² + 12²) = √(256 + 144) = √400 = 20