остроугольный и равнобедренный.
Объяснение:
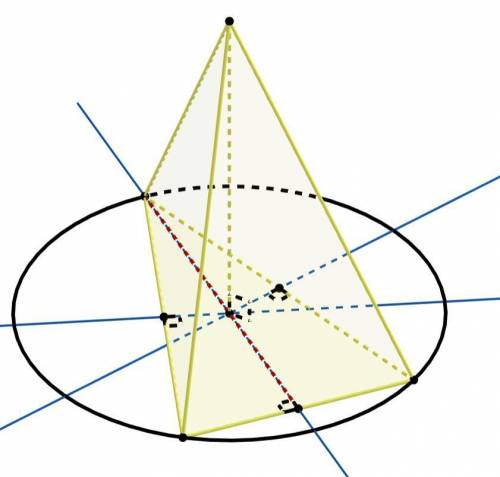
Если боковые рёбра пирамиды составляют равные углы с плоскостью основания, то основанием высоты пирамиды является центр окружности описанной около многоугольника из основания.
Центр окружности описанной около треугольника лежит внутри треугольника, если он остроугольный.
Так же этот центр лежит на пересечении серединных перпендикуляров к сторонам треугольника. Если центр описанной окружности лежит на одной высоте треугольника, то эта высота лежит на серединном перпендикуляре. А значит высота одновременно является и медианой. Тогда треугольник равнобедренный.
1) Тр. КОМ - прямоугольный (диагонали в ромбе пересекаются и перпендикулярны)
Значит, угол КОМ=90 гр.
2) Угол МKP = углу MNP =80 гр. (прот. углы ромба равны)
Угол MKO= угол MNP/2= 80/2=40 гр.
3) Угол KMO = 90 гр. - угол MNP = 90-40=50 (сумма острых угол в прямоугольном треугольнике равна 90 гр.)
2.
1) Тр. ABM - равнобедренный (по условию AB=AM)
Значит, углы при основании равны. Угол BAM=углу BMA
Т.к. BC || AD (прот. стороны параллелограмма), то угол ВМА=углу MAD (накрест лежащие углы при параллельных прямых)
Следовательно, угол BAM=углу МАD, значит АМ - биссектриса
2) АВ=CD=8 (прот. стороны параллелограмма)
АВ=АМ=8 (по условию)
ВС=АМ+МС=8+4=12
P= 8+8+12+12=40