
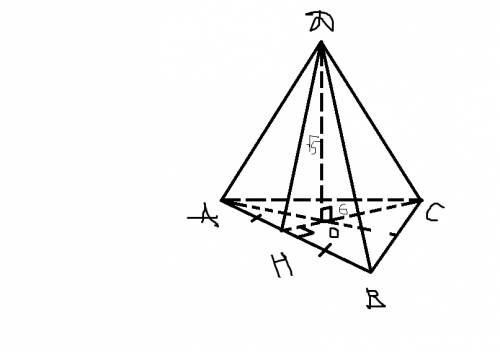
Рассмотрим треугольниу ABC-равносторонний(т.к.DABCD-прав. пирамида) OH=CH/3=6/3=2 (см)(в точке пересечения медианы делятся в отношении 2:1 от вершины)
Рассм. треуг. ODH-прямоуг. По теореме Пифагора DH=корень из DO^2+OH^2=корень из 5+4=корень из 9=3 (см)
Sпп=Sбп+Sосн
Рассм. треуг BCH-прямоуг.
sinB=MC/BC
sin60=6/BC
BC=6/(корень из 3/2)(под корнем только 3)=12/корень из 3=12 корней из 3/3=4 корня из 3(см)
Pосн=3*4 корня из 3=12 корней из 3 (см)
Sбп=1/2*DH*Pосн
Sбп=1/2*3*12 корней из 3=18корней из 3(см^2)
Sосн=1/2*CH*AB=1/2*6*4 корня из 3=12корней из3 (см^2)
Sпп=18корней из 3+12 корней из 3= 30 корней из3 (см^2)
1) Высота ромба перпендикулярна обеим противолежащим сторонам. -- угол СВЕ=90°, угол FВЕ=СВЕ-CBF=90°-30°=60°⇒
∠ВСF=30°
Противоположные углы параллелограмма равны. ⇒ ВЕ противолежит углу 30°, гипотенуза АВ треугольника АВЕ=2•6=12 см
Все стороны ромба равны ⇒
Р=12•4=48 см
———
2) Обозначим наклонные ВА и ВС;
ВН - расстояние от т.В до прямой. ВА=22 см, угол АВС=45°
ВН⊥АС.
Сумма острых углов прямоугольного треугольника равна 90°⇒
∆ АВН - равнобедренный.
ВН=АВ•sin45°=11√2
Из прямоугольного ∆ ВСН гипотенуза
ВС=√(BH²+CH²)=√(242+82)=18 см