Как расположены данные прямые?
Объяснение:
1. {4х+5у−1=0 ,а₁=4 ,в₁=5,
{12х +15у−8=0 ,а₂=12 ,в₂=15.
Проверим условие параллельности 4:12=5:15 , 1/3=1/3 верно, значит прямые параллельны.
2. {14х+2у−24=0 ,а₁=14 ,в₁=2 ,
{8х−56у+1=0 ,а₂=8 ,в₂=-56.
Проверим условие параллельности 14:8=2:(-56) , 7/4=-1/28 неверно, значит прямые не параллельны.
Проверим условие перпендикулярности 14*8=-(-56*2) ,112=112 верно, значит прямые перпендикулярны .
3.{12х+55у−19=0 , а₁=12 ,в₁=55 ,
{7х−12у+1=0 ,а₂=7 ,в₂=-12.
Вижу сразу , что не параллельны, т.к числа не пропорциональны и.Не перпендикулярны , т.к произведения разных знаков. Значит пересекаются .
================================================
PS. Если прямые заданы в виде а₁х+ в₁у+с₁=0, а₂х+ву₂+с₂=0 , то
- прямые параллельны если 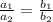 ;
;
-перпендикулярны если а₁*а₂ = в₁*в₂ .
1).
Перпендикулярные плоскости образуют двугранный угол, линейный угол которого образован лучами с общим началом на ребре двугранного угла, проведенными в его гранях перпендикулярно ребру.
Здесь грани - плоскости треугольников АВС и АВС1, ребро двугранного угла – АВ.
НС⊥АВ; НС1⊥АВ, угол СНС1=90° по условию.
∆ АВС и ∆ АВС1 равнобедренные прямоугольные, углы при их общем основании АВ равны 45°, ⇒ они равны по 2-признаку равенства треугольников.
∆ СНС1- прямоугольный. Его катеты равны высотам=медианам равных треугольников. Следовательно, он равнобедренный.
Медиана прямоугольного треугольника равна половине гипотенузы. ⇒
НС=НС1=3
СС1=3•sin45°=3√2 см
2)
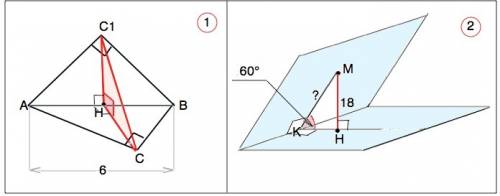
Расстояние от точки М до плоскости - длина отрезка МН, проведенного между ними перпендикулярно. МН=18
Расстояние от точки М до ребра двугранного угла - длина отрезка МК, проведенного между ними перпендикулярно.
∆ МКН - прямоугольный. Его гипотенуза МК=МН:sin60°
MK=18:(√3/2)=12√3
Проще можно методом последовательного перехода в разные плоскости:
сначала определить в плане, а затем в вертикальных плоскостях, включающих исходную линию с точками В и С, а затем в перпендикулярной плоскости (см. приложение)