Доказательство в объяснении и приложении.
Объяснение:
Если прямые I1 и I2 - касательные к соответствующим окружностям, то ∠ВАС равен половине дуги АС (большой окружности) по свойству угла между хордой и касательной. ∠ADC равен половине дуги АС (большой окружности) как вписанный, опирающийся на эту дугу. =>
∠АDC = ∠ВАC.
∠ACD равен половине дуги АС (малой окружности) по свойству угла между хордой и касательной. ∠AВC равен половине дуги АС (малой окружности) как вписанный, опирающийся на эту дугу. =>
∠АСD = ∠ABC.
В треугольнике ACD ∠CАD = 180 - ∠АСD - ∠ADC.
В треугольнике AВC ∠АСВ= 180 - ∠АBC - ∠BAC. =>
∠CАD = ∠АСВ. Это внутренние накрест лежащие углы про прямыхI3 и I4 и секущей АС => прямые I3 и I4 - параллельные, что и требовалось доказать.
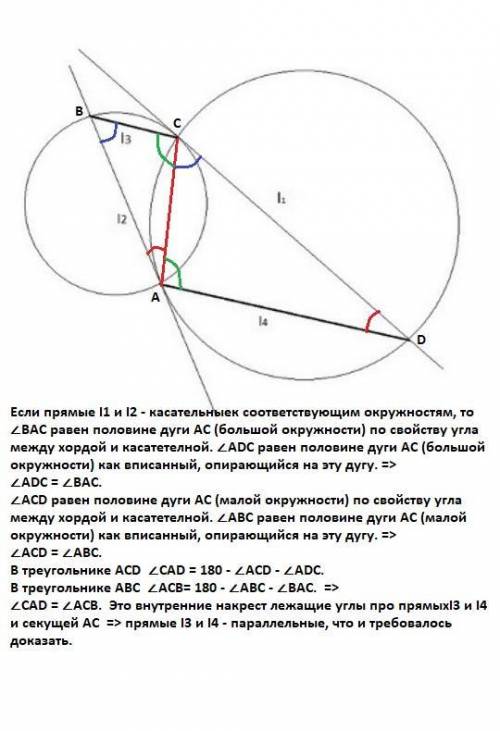
Доказательство в объяснении и приложении.
Объяснение:
Если прямые I1 и I2 - касательные к соответствующим окружностям, то ∠ВАС равен половине дуги АС (большой окружности) по свойству угла между хордой и касательной. ∠ADC равен половине дуги АС (большой окружности) как вписанный, опирающийся на эту дугу. =>
∠АDC = ∠ВАC.
∠ACD равен половине дуги АС (малой окружности) по свойству угла между хордой и касательной. ∠AВC равен половине дуги АС (малой окружности) как вписанный, опирающийся на эту дугу. =>
∠АСD = ∠ABC.
В треугольнике ACD ∠CАD = 180 - ∠АСD - ∠ADC.
В треугольнике AВC ∠АСВ= 180 - ∠АBC - ∠BAC. =>
∠CАD = ∠АСВ. Это внутренние накрест лежащие углы про прямыхI3 и I4 и секущей АС => прямые I3 и I4 - параллельные, что и требовалось доказать.

cosA = AC / AB =>
AC = AB*cosA
осталось найти AB...
по определению синуса
sinA = CB / AB
AB = CB / sinA
основное тригонометрическое тождество позволяет найти синус, если известен косинус (и наоборот...)))
(sinA)^2 + (cosA)^2 = 1
(sinA)^2 = 1 - 1/5 = 4/5
sinA = 2 / V5
AB = 6*V5 / 2 = 3V5
AC = 3V5 / V5 = 3